题目内容
在空间四边形ABCD中,M、N分别是AD、BC的中点,若AB-CD=1,且AB⊥CD,则MN的长度是 .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:首先把空间问题转化为平面问题,通过做平行线得到直角三角形,进一步解直角三角形求得结果.
解答:
解:在空间四边形ABCD中,M、N分别是AD、BC的中点,若AB=CD=1,且AB⊥CD,
则:取BD的中点E,连接ME,NE,
得到:ME⊥NE,ME=
AB=
,NE=
CD=
则在Rt△MNE中,MN2=ME2+NE2
解得:MN=
故答案为:

则:取BD的中点E,连接ME,NE,
得到:ME⊥NE,ME=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则在Rt△MNE中,MN2=ME2+NE2
解得:MN=
| ||
| 2 |
故答案为:
| ||
| 2 |

点评:本题考查的知识要点:异面直线所成的角的应用,勾股定理的应用,属于基础题型.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
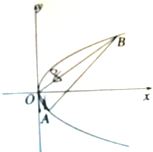 如图,已知抛物线有一个内接直角三角形,直角顶点在原点,两直角边分别为1和8,求抛物线方程.
如图,已知抛物线有一个内接直角三角形,直角顶点在原点,两直角边分别为1和8,求抛物线方程.