题目内容
若(2m+1)
>(m2+m-1)
,则实数m的取值范围是 .
| 1 |
| 2 |
| 1 |
| 2 |
考点:有理数指数幂的化简求值
专题:不等式的解法及应用
分析:由(2m+1)
>(m2+m-1)
,可得:(2m+1)>(m2+m-1)>0,解得实数m的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵(2m+1)
>(m2+m-1)
,
∴(2m+1)
>(m2+m-1)
,
∴(2m+1)>(m2+m-1)>0,
解得:m∈[
,2),
故答案为:[
,2)
| 1 |
| 2 |
| 1 |
| 2 |
∴(2m+1)
| 1 |
| 2 |
| 1 |
| 2 |
∴(2m+1)>(m2+m-1)>0,
解得:m∈[
| ||
| 2 |
故答案为:[
| ||
| 2 |
点评:本题考查的知识点是有理数指数幂的化简求值,根式不等式的解法,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x||x|<2},B={x|x2>1},则A∩B=( )
| A、(1,2) |
| B、(-2,-1) |
| C、(-2,-1)∪(1,2) |
| D、∅ |
已知向量
、
是平面α内的两个不相等的非零向量,非零向量
在直线l上,则
•
=0,且
•
=是l⊥α的( )
| a |
| b |
| c |
| c |
| a |
| c |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
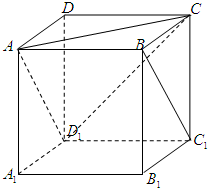 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题: