题目内容

已知y=f（x）是定义在（-∞，0）∪（0，+∞）上的奇函数，当x＞0时，f（x）=log2x，
（1）求函数f（x）解析式并画出函数图象；
（2）请结合图象直接写出不等式xf（x）＜0的解集．
考点：对数函数的图像与性质
专题：函数的性质及应用
分析：（1）当x＜0时，则-x＞0，转化为已知的范围求解即可．
（2）画出图象，利用图象写出解集．
解答： 解：（ 1）当x＜0时，则-x＞0，f（-x）=log2（-x），
又y=f（x）是定义在R上的奇函数
∴f（x）=-f（-x）=-log2（-x）
∴f(x)=
log2x， x＞0
-log2(-x)，  x＜0
，

（2）式xf（x）＜0的解集为：（-1，0）∪（0，1），
点评：本题考查了函数的性质，定义，图象，属于中档题，注意识图理解．
练习册系列答案
相关题目
判断函数y=x3+x的单调性和奇偶性，并证明你的结论．
已知全集U=R，函数f（x）=log3（x2+x-2）的定义域为A，关于x的不等式|x-2|＞a的解集为B．
（Ⅰ）若命题：x∈B是命题x∈A成立的充分不必要条件，求实数a的取值范围；
（Ⅱ）若A∪B=U，求实数a的取值范围．
椭圆C的焦点分别为F1（-1，0）F2（1，0），P（1，
2
2
）是椭圆上的一个点
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）设原点为O，斜率为
2
2
的直线l过点F1且与椭圆C相交于A、B两点，求△AOB的面积．
已知梯形ABCD中，AD=1，AB=2，∠DAB=
π
3
，DC∥AB，若
DE
=λ
DC
，则当
AE
•
BD
=-
3
4
时，λ=
 
．
2sin5°-cos25°
sin25°
的值是
 
．
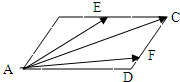如图所示，在平行四边形ABCD中，E为BC的中点，F为CD的四分之一点，设
AC
=m
AE
+N
AF
，则m+n=
 
．
已知函数f（x）=x2-2|x|．
（1）画出该函数的图象；
（2）求出函数的最值；
（3）若函数y=m的图象与函数y=f（x）的图象有四个不同的交点，求实数m的取值范围．
设函数f（x）=
3
cos2ωx+sinωxcosωx（ω，a∈R），已知f（x）的图象在y轴右侧的第一个最高点的横坐标为
π
6
．
（1）求ω的值；
（2）若函数y=f（x）的图象按向量
b
=（
π
6
，
3
2
）平移后得到函数y=g（x）的图象，求y=g（x）在区间[0，
π
2
]的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网