题目内容
已知
=（4，-3），
=（2，2），若
+t
与
的夹角为45°，求实数t的值．
| a |
| b |
| a |
| b |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据向量数量积的坐标公式建立方程即可得到结论．
解答：
解：∵
=（4，-3），
=（2，2），
∴
+t
=（4+2t，-3+2t），
∴（
+t
）•
=8+4t-6+4t=2+8t，
∴|
+t
|=
，|
|=2
，
∵
+
与
的夹角为45°，
∴2+8t＞0，即t＞-
∴cos45°=
=
=
平方整理得2t2+t-6=0
即（2t-3）（t+2）=0
解得t=-2（舍去）或t=
，
故t的值为
| a |
| b |
∴
| a |
| b |
∴（
| a |
| b |
| b |
∴|
| a |
| b |
| 8t2+4t+25 |
| b |
| 2 |
∵
| a |
| b |
| b |
∴2+8t＞0，即t＞-
| 1 |
| 4 |
∴cos45°=
(
| ||||||
|
|
| 2+8t | ||||
|
| ||
| 2 |
平方整理得2t2+t-6=0
即（2t-3）（t+2）=0
解得t=-2（舍去）或t=
| 3 |
| 2 |
故t的值为
| 3 |
| 2 |
点评：本题主要考查数量积的应用，运算量较大，要求熟练掌握数量积的坐标公式．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
设偶函数f（x）的定义域为R，当x∈[0，+∞）时，f（x）是减函数，则f（-2），f（π），f（-1）的大小关系是（ ）
| A、f（-2）＜f（-1）＜f（π） |
| B、f（-2）＜f（π）＜f（-1） |
| C、f（-2）＞f（π）＞f（-1） |
| D、f（-1）＞f（-2）＞f（π） |
函数f（x）=
的定义域是（ ）
| 7+x |
| A、[-7，+∞） |
| B、（-∞，-7] |
| C、[0，+∞） |
| D、R |
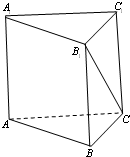如图，正三棱柱的底面边长为1，体积为