题目内容
已知函数y=x2+2mx+m+6与x轴的两个交点A、B位于原点的同侧,求实数m的取值范围 .
考点:一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:根据二次函数根的发布,建立条件关系即可得到结论.
解答:
解:∵函数y=x2+2mx+m+6与x轴的两个交点A、B位于原点的同侧,
∴方程x2+2mx+m+6=0的两个根同号,
设f(x)=x2+2mx+m+6,
则满足
,
即
,
∴
,
即m≥3或-6<m≤-2.
故答案为:m≥3或-6<m≤-2.
∴方程x2+2mx+m+6=0的两个根同号,
设f(x)=x2+2mx+m+6,
则满足
|
即
|
∴
|
即m≥3或-6<m≤-2.
故答案为:m≥3或-6<m≤-2.
点评:本题主要考查一元二次方程根的发布,利用函数和方程之间的关系,建立条件关系是解决本题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
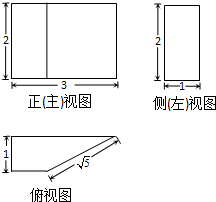
某几何体的三视图如图所示,则该几何体的体积为( )

| A、2 | ||
B、
| ||
| C、4 | ||
| D、5 |
设xi∈N(i=1,2,3,4,5,6…),则满足x1<x2<x3<x4<10的有序数组(x1,x2,x3,x4)的个数为( )
| A、126 | B、3024 |
| C、210 | D、5040 |