题目内容
 一个正三棱柱的三视图如图所示,这个三棱柱的侧(左)视图的面积为6
一个正三棱柱的三视图如图所示,这个三棱柱的侧(左)视图的面积为6| 3 |
| A、12 | ||
| B、16 | ||
C、8
| ||
D、12
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:设此三棱柱底面边长为a,高为h,根据左视图的面积为6
,可得三棱柱的侧棱长为H,把数据代入棱柱的体积公式计算.
| 3 |
解答:
解:设此三棱柱底面边长为a,高为h,则由图示知
a=2
,
∴a=4,
侧视图面积为2
×h=6
,
∴h=3,
这个三棱柱的体积为
×42×h=12
.
故选:D.
| ||
| 2 |
| 3 |
∴a=4,
侧视图面积为2
| 3 |
| 3 |
∴h=3,
这个三棱柱的体积为
| ||
| 4 |
| 3 |
故选:D.
点评:本题考查了由三视图求几何体的体积,关键是对几何体正确还原,并根据三视图的长度求出几何体的几何元素的长度,考查了空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )
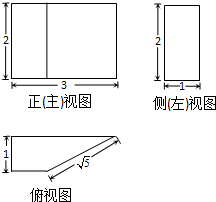

| A、2 | ||
B、
| ||
| C、4 | ||
| D、5 |
设集合U={1,2,3,4,5},A={2,3,5},则∁UA=( )
| A、{5} |
| B、{1,4} |
| C、{2,3} |
| D、{2,3,5} |
设xi∈N(i=1,2,3,4,5,6…),则满足x1<x2<x3<x4<10的有序数组(x1,x2,x3,x4)的个数为( )
| A、126 | B、3024 |
| C、210 | D、5040 |
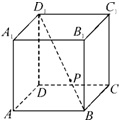 如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有
如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有 唐徕回中随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100],
唐徕回中随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100],