题目内容
以下判断正确的是( )
| A、函数y=f(x)为R上的可导函数,则“f′(x0)=0”是“x0为函数f(x)极值点”的充要条件 |
| B、“a=1”是“直线ax+y-1=0与直线x+ay+1=0平行”的充要条件 |
| C、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
| D、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” |
考点:命题的真假判断与应用
专题:探究型,简易逻辑
分析:A,由极值点的定义判断;B,“直线ax+y-1=0与直线x+ay+1=0平行”的充要条件是a2=1,即a=±1;C,据正弦定理,可知正确;D,命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1≥0”.
解答:
解:A,不正确,点x0为f(x)的极值点由必须满足两个条件一是f′(x0)=0,二是两侧的正负相异;
B,正确,“直线ax+y-1=0与直线x+ay+1=0平行”的充要条件是a2=1且a≠-1,即a=1;
C,命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为“在△ABC中,若sinA>sinB,则A>B”,根据正弦定理,可知不是假命题;
D,不正确,命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1≥0”.
故选:B.
B,正确,“直线ax+y-1=0与直线x+ay+1=0平行”的充要条件是a2=1且a≠-1,即a=1;
C,命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为“在△ABC中,若sinA>sinB,则A>B”,根据正弦定理,可知不是假命题;
D,不正确,命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1≥0”.
故选:B.
点评:本题考查命题的真假判断与应用,考查简易逻辑基本概念,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )
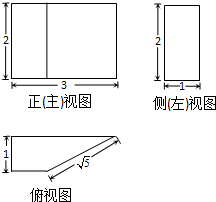

| A、2 | ||
B、
| ||
| C、4 | ||
| D、5 |
设xi∈N(i=1,2,3,4,5,6…),则满足x1<x2<x3<x4<10的有序数组(x1,x2,x3,x4)的个数为( )
| A、126 | B、3024 |
| C、210 | D、5040 |
函数h(x)=2sin(2x+
)的图象与函数f(x)的图象关于点(0,1)对称,则函数f(x)可由h(x)经过怎样的变换得到( )
| π |
| 4 |
A、向上平移2个单位,向右平移
| ||
B、向上平移2个单位,向左平移
| ||
C、向下平移2个单位,向右平移
| ||
D、向下平移2个单位,向左平移
|