题目内容
已知函数f(x)=alnx+
+x,其中a∈R.
(Ⅰ)若a=1,求函数f(x)的极值点;
(Ⅱ)若f(x)在区间[1,+∞)内单调递增,求实数a的取值范围.
| 2 |
| x |
(Ⅰ)若a=1,求函数f(x)的极值点;
(Ⅱ)若f(x)在区间[1,+∞)内单调递增,求实数a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:
分析:(1)先求函数的导函数f′(x),再解不等式f′(x)>0,得函数的单调增区间,解不等式f′(x)<0得函数的单调减区间,最后由极值定义求得函数极值.
(2)通过已知条件,求出函数的导数,转化导数大于等于0恒成立,得到a的表达式,求出a的最小值即可.
(2)通过已知条件,求出函数的导数,转化导数大于等于0恒成立,得到a的表达式,求出a的最小值即可.
解答:
解:(1)当x=1时,f(x)=lnx+
+x,(x>0),f′(x)=
-
+1,
∴f(x)的单调递减区间为(0,1),单调增区间为(1,+∞),
∴当x=1时,f(x)有极小值.
(2)由函数f(x)=alnx+
+x,得f′(x)=
-
+1,
若函数f(x)为[1,+∞)上的单调增函数,则f′(x)≥0在[1,+∞)上恒成立,
即不等式
-
+1≥0在[1,+∞)上恒成立.也即a≥
-x在[1,+∞)上恒成立.
又g(x)=
-x在[1,+∞)上为减函数,g(x)max=g(1)=1.所以a≥1.
| 2 |
| x |
| 1 |
| x |
| 2 |
| x2 |
∴f(x)的单调递减区间为(0,1),单调增区间为(1,+∞),
∴当x=1时,f(x)有极小值.
(2)由函数f(x)=alnx+
| 2 |
| x |
| a |
| x |
| 2 |
| x2 |
若函数f(x)为[1,+∞)上的单调增函数,则f′(x)≥0在[1,+∞)上恒成立,
即不等式
| a |
| x |
| 2 |
| x2 |
| 2 |
| x |
又g(x)=
| 2 |
| x |
点评:本题考查函数与导函数的关系,函数的单调性与导数的关系,通过函数的导数求解函数极值,考查转化思想与计算能力.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )
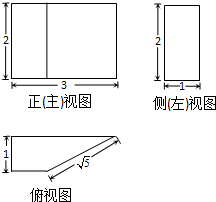

| A、2 | ||
B、
| ||
| C、4 | ||
| D、5 |
 唐徕回中随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100],
唐徕回中随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100],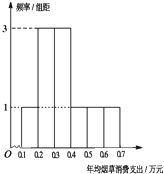 某地区共有100万人,现从中随机抽查800人,发现有700人不吸烟,100人吸烟.这100位吸烟者年均烟草消费支出情况的频率分布直方图如图.将频率视为概率,回答下列问题:
某地区共有100万人,现从中随机抽查800人,发现有700人不吸烟,100人吸烟.这100位吸烟者年均烟草消费支出情况的频率分布直方图如图.将频率视为概率,回答下列问题: