题目内容
设X为随机变量,它的分布列如图所示,则V(X)= .


考点:离散型随机变量及其分布列
专题:概率与统计
分析:先利用分布列的性质求出t,再求出E(X),由此能求出V(X).
解答:
解:由题意知t=1-
-
=
,
∴E(X)=(-1)×
+0×
+1×
=-
,
∴V(X)=(-1+
)2×
+(0+
)2×
+(1+
)2×
=
.
故答案为:
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
∴E(X)=(-1)×
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
∴V(X)=(-1+
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 6 |
| 5 |
| 9 |
故答案为:
| 5 |
| 9 |
点评:本题考查离散型随机变量的方差的求法,是基础题,解题时要认真审题,注意分布列的性质的合理运用.

练习册系列答案
相关题目
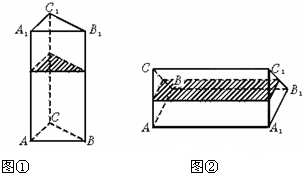 如图①是一个正三棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面.请问图①中容器内水面的高度是多少?
如图①是一个正三棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面.请问图①中容器内水面的高度是多少?