题目内容
5.平面α截半径为2的球O所得的截面圆的面积为π,则球心到O平面α的距离为( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
分析 先求截面圆的半径,然后求出球心到截面的距离.
解答 解:∵截面圆的面积为π,
∴截面圆的半径是1,
∵球O半径为2,
∴球心到截面的距离为$\sqrt{{R}^{2}-{r}^{2}}=\sqrt{3}$.
故选:A
点评 本题考查球的性质、球的体积、点到平面的距离,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
15.已知等差数列{an}满足a3+a13-a8=2,则{an}的前15项和S15=( )
| A. | 60 | B. | 30 | C. | 15 | D. | 10 |
13.在等比数列{an}中,已知${a_1}+{a_2}=-\frac{3}{2},{a_4}+{a_5}=12$,则数列是( )
| A. | 递增数列 | B. | 递减数列 | C. | 摆动数列 | D. | 常数列 |
14.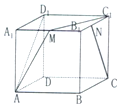 在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,那么直线AM与CN所成角的余弦值是( )
在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,那么直线AM与CN所成角的余弦值是( )
 在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,那么直线AM与CN所成角的余弦值是( )
在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,那么直线AM与CN所成角的余弦值是( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |