题目内容
17.函数f(x)=x2-2x+a在区间(1,3)内有一个零点,则实数a的取值范围是( )| A. | (-3,0) | B. | (-3,1) | C. | (-1,3) | D. | (-1,1) |
分析 由题意知,函数f(x)在区间(1,3)内有一个零点,它的对称轴为x=1,得出不等式组,解出即可.
解答 解:∵令f(x)=x2-2x+a,它的对称轴为x=1,
∴函数f(x)在区间(1,3)单调递增,
∵方程x2-2x+a=0在区间(1,3)内有一个零点,
∴函数f(x)在区间(1,3)内与x轴有一个交点,
根据零点存在性定理得出:$\left\{\begin{array}{l}{f(1)<0}\\{f(3)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{1-2+a<0}\\{9-6+a>0}\end{array}\right.$
解得:-3<a<1,
故选:B.
点评 此题主要考查函数的零点以及二次函数的性质问题,是一道基础题,容易得出答案.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8.若集合A={-1,2},B={0,1},则集合{z|z=x+y,x∈A,y∈B}的子集共有( )
| A. | 2个 | B. | 4个 | C. | 8个 | D. | 16个 |
5.已知数列{an}为等差数列,若a12+a102≤25恒成立,则a1+3a7的取值范围为( )
| A. | [-5,5] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-10,10] | D. | [-10$\sqrt{2}$,10$\sqrt{2}$] |
12.在等腰三角形ABC中,∠A=150°,AC=AB=1,则$\overrightarrow{AB}•\overrightarrow{BC}$=( )
| A. | $-\frac{{\sqrt{3}}}{2}-1$ | B. | $-\frac{{\sqrt{3}}}{2}+1$ | C. | $\frac{{\sqrt{3}}}{2}-1$ | D. | $\frac{{\sqrt{3}}}{2}+1$ |
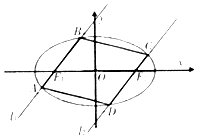 如图,过椭圆C:$\frac{{x}^{2}}{4}$+y2=1的左右焦点F1,F2分别作直线l1,l2交椭圆于A,B与C,D,且l1∥l2.
如图,过椭圆C:$\frac{{x}^{2}}{4}$+y2=1的左右焦点F1,F2分别作直线l1,l2交椭圆于A,B与C,D,且l1∥l2.