题目内容
15.在极坐标系中,点(2,$\frac{π}{3}$)到圆ρ=-2cosθ的圆心的距离为$\sqrt{7}$.分析 先将极坐标方程化为直角方程,然后再计算点(2,$\frac{π}{3}$)到圆ρ=-2cosθ的圆心的距离.
解答 解:∵在极坐标系中,ρ=-2cosθ,∴x=pcosθ,y=psinθ,消去p和θ得,
∴(x+1)2+y2=1,
∴圆心的直角坐标是(-1,0),半径长为1.
∴点(2,$\frac{π}{3}$)在直角坐标为(1,$\sqrt{3}$),
∴点(2,$\frac{π}{3}$)到圆ρ=-2cosθ的圆心的距离是d=$\sqrt{4+3}$=$\sqrt{7}$,
故答案为$\sqrt{7}$
点评 此题考查极坐标方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解.

练习册系列答案
相关题目
5.已知数列{an}中,a1=2,an+1=an+n(n∈N+),则a4的值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
6.设函数f(x)=sin(2x+$\frac{π}{6}$)+$\sqrt{3}$cos(2x+$\frac{π}{6}$),则( )
| A. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{4}$对称 | |
| B. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{2}$对称 | |
| C. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{4}$对称 | |
| D. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{2}$对称 |
10.已知P是边长为4的正△ABC的边BC上的动点,则$\overrightarrow{AP}•(\overrightarrow{AB}+\overrightarrow{AC})$( )
| A. | 最大值为16 | B. | 是定值24 | C. | 最小值为4 | D. | 是定值4 |
20.在△ABC中,点D满足$\overrightarrow{BC}$=3$\overrightarrow{BD}$,则( )
| A. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
7.如果圆柱的轴截面的周长l为定值,则圆柱体积的最大值为( )
| A. | ($\frac{l}{6}$)3π | B. | ($\frac{l}{3}$)3π | C. | ($\frac{l}{4}$)3π | D. | $\frac{1}{4}$($\frac{l}{4}$)3π |
17.函数f(x)=x2-2x+a在区间(1,3)内有一个零点,则实数a的取值范围是( )
| A. | (-3,0) | B. | (-3,1) | C. | (-1,3) | D. | (-1,1) |
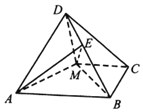 如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.