题目内容
2.椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$的左、右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|的值为$\frac{5}{4}$.分析 由已知求出椭圆的焦点分别为F1(-3,0)、F2(3,0),△ABF2的内切圆半径r=$\frac{1}{2}$,△ABF2的面积S=$\frac{1}{2}$(|AB|+|AF2|+|BF2|)×r=5,再由△ABF2的面积S=${S}_{△A{F}_{1}{F}_{2}}+{S}_{△B{F}_{1}{F}_{2}}$=4|y2-y1|,由此能求出|y1-y2|的值.
解答 解:椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$中,a2=25且b2=16,
∴a=5,c=$\sqrt{25-16}=3$,
∴椭圆的焦点分别为F1(-3,0)、F2(3,0),
设△ABF2的内切圆半径为r,
∵△ABF2的内切圆周长为π,∴r=$\frac{1}{2}$,
根据椭圆的定义,得|AB|+|AF2|+|BF2|=(|AF1|+|AF2|)+(|BF1|+|BF2|)=4a=20.
∴△ABF2的面积S=$\frac{1}{2}$(|AB|+|AF2|+|BF2|)×r=$\frac{1}{2}$×20×$\frac{1}{2}$=5,
又∵△ABF2的面积S=${S}_{△A{F}_{1}{F}_{2}}+{S}_{△B{F}_{1}{F}_{2}}$=$\frac{1}{2}$×|y1|×|F1F2|+$\frac{1}{2}$×|y2|×|F1F2|
=$\frac{1}{2}$×(|y1|+|y2|)×|F1F2|=4|y2-y1|(A、B在x轴的两侧),
∴4|y1-y2|=5,解得|y1-y2|=$\frac{5}{4}$.
故答案为:$\frac{5}{4}$.
点评 本题考查两点纵坐标之差的绝对值的求法,考查椭圆性质的合理运用,是中档题.

练习册系列答案
相关题目
20.在△ABC中,点D满足$\overrightarrow{BC}$=3$\overrightarrow{BD}$,则( )
| A. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
13.随机调查某社区80个人,以研究这一社区居民在17:00-21:00时间段的休闲方式是否与性别有关,得到下面的数据表:
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分布列和期望;
(2)根据以上数据,能否有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系?
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 10 | 30 |
| 女 | 45 | 5 | 50 |
| 合计 | 65 | 15 | 80 |
(2)根据以上数据,能否有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系?
10.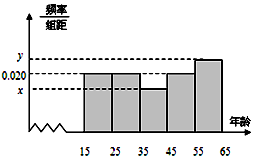 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
(Ⅰ)写出其中的a、b、n及x和y的值;
(Ⅱ)若从第1,2,3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,用X表示其中是第3组的人数,求X的分布列和期望.
 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.(Ⅰ)写出其中的a、b、n及x和y的值;
(Ⅱ)若从第1,2,3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,用X表示其中是第3组的人数,求X的分布列和期望.
| 组号 | 分组 | 喜爱人数 | 喜爱人数占本组的频率 |
| 第1组 | [15,25) | a | 0.10 |
| 第2组 | [25,35) | b | 0.20 |
| 第3组 | [35,45) | 6 | 0.40 |
| 第4组 | [45,55) | 12 | 0.60 |
| 第5组 | [55,65) | 20 | 0.80 |
17.函数f(x)=x2-2x+a在区间(1,3)内有一个零点,则实数a的取值范围是( )
| A. | (-3,0) | B. | (-3,1) | C. | (-1,3) | D. | (-1,1) |
 《九章算术》是我国古代数学著作,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积及堆放的米各为多少?”已知一斛米的体积约为1.62立方尺,由此估算出堆放的米约有( )
《九章算术》是我国古代数学著作,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积及堆放的米各为多少?”已知一斛米的体积约为1.62立方尺,由此估算出堆放的米约有( )