题目内容
8.若集合A={-1,2},B={0,1},则集合{z|z=x+y,x∈A,y∈B}的子集共有( )| A. | 2个 | B. | 4个 | C. | 8个 | D. | 16个 |
分析 求出集合z,从而求出z的子集的个数即可.
解答 解:A={-1,2},B={0,1},
则集合{z|z=x+y,x∈A,y∈B}={-1,0,2,3},
其子集的个数是24=16,
故选:D.
点评 本题考查了集合的子集问题,是一道基础题.

练习册系列答案
相关题目
6.设函数f(x)=sin(2x+$\frac{π}{6}$)+$\sqrt{3}$cos(2x+$\frac{π}{6}$),则( )
| A. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{4}$对称 | |
| B. | y=f(x)在(0,$\frac{π}{2}$)单调递增,其图象关于直线x=$\frac{π}{2}$对称 | |
| C. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{4}$对称 | |
| D. | y=f(x)在(0,$\frac{π}{2}$)单调递减,其图象关于直线x=$\frac{π}{2}$对称 |
7.如果圆柱的轴截面的周长l为定值,则圆柱体积的最大值为( )
| A. | ($\frac{l}{6}$)3π | B. | ($\frac{l}{3}$)3π | C. | ($\frac{l}{4}$)3π | D. | $\frac{1}{4}$($\frac{l}{4}$)3π |
13.随机调查某社区80个人,以研究这一社区居民在17:00-21:00时间段的休闲方式是否与性别有关,得到下面的数据表:
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分布列和期望;
(2)根据以上数据,能否有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系?
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 10 | 30 |
| 女 | 45 | 5 | 50 |
| 合计 | 65 | 15 | 80 |
(2)根据以上数据,能否有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系?
17.函数f(x)=x2-2x+a在区间(1,3)内有一个零点,则实数a的取值范围是( )
| A. | (-3,0) | B. | (-3,1) | C. | (-1,3) | D. | (-1,1) |
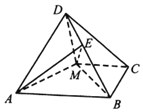 如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.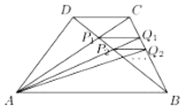 梯形ABCD中AB∥CD,对角线AC,BD交于P1,过P1作AB的平行线交BC于点Q1,AQ1交BD于P2,过P2作AB的平行线交BC于点Q2,….,若AB=a,CD=b,则PnQn=$\frac{ab}{a+nb},n∈N*$(用a,b,n表示)
梯形ABCD中AB∥CD,对角线AC,BD交于P1,过P1作AB的平行线交BC于点Q1,AQ1交BD于P2,过P2作AB的平行线交BC于点Q2,….,若AB=a,CD=b,则PnQn=$\frac{ab}{a+nb},n∈N*$(用a,b,n表示)