题目内容
5.已知数列{an}为等差数列,若a12+a102≤25恒成立,则a1+3a7的取值范围为( )| A. | [-5,5] | B. | [-5$\sqrt{2}$,5$\sqrt{2}$] | C. | [-10,10] | D. | [-10$\sqrt{2}$,10$\sqrt{2}$] |
分析 利用等差数列的性质令a1=5cosθ,a10=5sinθ(0<θ<$\frac{π}{2}$),则d=$\frac{5}{9}$(sinθ-cosθ),问题转化为三角函数在定区间上求最值问题解决即可.
解答 解:由题意得,令a1=5cosθ,a10=5sinθ(0<θ<$\frac{π}{2}$),则d=$\frac{5}{9}$(sinθ-cosθ),
∴a1+3a7=10(sinθ+cosθ)=10$\sqrt{2}$sin(θ+$\frac{π}{4}$),
∴a1+3a7的取值范围为[-10$\sqrt{2}$,10$\sqrt{2}$],
故选:D.
点评 本题主要考查了等差数列的性质,借助三角函数,通过等价转化思想达到解决问题的目的,要体会这种换元法的解题思路,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.随机调查某社区80个人,以研究这一社区居民在17:00-21:00时间段的休闲方式是否与性别有关,得到下面的数据表:
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分布列和期望;
(2)根据以上数据,能否有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系?
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 10 | 30 |
| 女 | 45 | 5 | 50 |
| 合计 | 65 | 15 | 80 |
(2)根据以上数据,能否有99%的把握认为在17:00-21:00时间段的休闲方式与性别有关系?
10.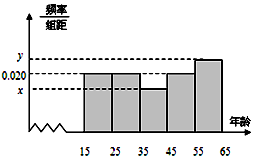 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
(Ⅰ)写出其中的a、b、n及x和y的值;
(Ⅱ)若从第1,2,3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,用X表示其中是第3组的人数,求X的分布列和期望.
 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.(Ⅰ)写出其中的a、b、n及x和y的值;
(Ⅱ)若从第1,2,3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,用X表示其中是第3组的人数,求X的分布列和期望.
| 组号 | 分组 | 喜爱人数 | 喜爱人数占本组的频率 |
| 第1组 | [15,25) | a | 0.10 |
| 第2组 | [25,35) | b | 0.20 |
| 第3组 | [35,45) | 6 | 0.40 |
| 第4组 | [45,55) | 12 | 0.60 |
| 第5组 | [55,65) | 20 | 0.80 |
17.函数f(x)=x2-2x+a在区间(1,3)内有一个零点,则实数a的取值范围是( )
| A. | (-3,0) | B. | (-3,1) | C. | (-1,3) | D. | (-1,1) |
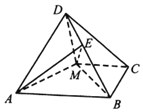 如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD=DM,且AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM. 《九章算术》是我国古代数学著作,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积及堆放的米各为多少?”已知一斛米的体积约为1.62立方尺,由此估算出堆放的米约有( )
《九章算术》是我国古代数学著作,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积及堆放的米各为多少?”已知一斛米的体积约为1.62立方尺,由此估算出堆放的米约有( )