题目内容
3.若某几何体的三视图如图所示,则此几何体的体积是( )
| A. | 24 | B. | 40 | C. | 36 | D. | 48 |
分析 几何体为三棱柱切去两个小棱锥得到的,用棱柱的体积减去两个小棱锥的体积即可.
解答 解:由三视图可知该几何体为三棱柱切去两个大小相等的小棱锥得到的,
三棱柱的底面为侧视图中三角形,底面积S=$\frac{1}{2}×4×3$=6,三棱柱的高h=8,∴V三棱柱=Sh=48,
切去的小棱锥的底面与棱柱的底面相同,小棱锥的高h′=2,∴V棱锥=$\frac{1}{3}$Sh′=4,
∴几何体的体积V=V三棱柱-2V棱锥=48-2×4=40.
故选:B.
点评 本题考查了常见几何体的三视图和体积计算,属于基础题.

练习册系列答案
相关题目
8.已知棱长为2,各面均为等边三角形的四面体,则其表面积为( )
| A. | 12 | B. | $2\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $\frac{4}{3}\sqrt{3}$ |
15.已知集合P={x|1<2x<2},Q={x|log${\;}_{\frac{1}{2}}$x>1},则P∩Q=( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2},1$) | C. | (-1,$\frac{1}{2}$) | D. | (0,1) |
12.为评估设备M生产某种零件的性能,从设备M生产零件的流水线上随机抽取100件零件最为样本,测量其直径后,整理得到下表:
经计算,样本的平均值μ=65,标准差=2.2,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为X,并根据以下不等式进行评判(p表示相应事件的频率):①p(μ-σ<X≤μ+σ)≥0.6826.②P(μ-σ<X≤μ+2σ)≥0.9544③P(μ-3σ<X≤μ+3σ)≥0.9974.评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙,若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.试判断设备M的性能等级.
(2)将直径小于等于μ-2σ或直径大于μ+2σ的零件认为是次品
(i)从设备M的生产流水线上随意抽取2件零件,计算其中次品个数Y的数学期望EY;
(ii)从样本中随意抽取2件零件,计算其中次品个数Z的数学期望EZ.
| 直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
| 件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为X,并根据以下不等式进行评判(p表示相应事件的频率):①p(μ-σ<X≤μ+σ)≥0.6826.②P(μ-σ<X≤μ+2σ)≥0.9544③P(μ-3σ<X≤μ+3σ)≥0.9974.评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙,若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.试判断设备M的性能等级.
(2)将直径小于等于μ-2σ或直径大于μ+2σ的零件认为是次品
(i)从设备M的生产流水线上随意抽取2件零件,计算其中次品个数Y的数学期望EY;
(ii)从样本中随意抽取2件零件,计算其中次品个数Z的数学期望EZ.

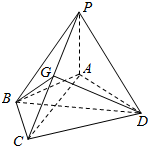 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,G为线段PC上的点,∠ABC=120°
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,G为线段PC上的点,∠ABC=120°