题目内容
11.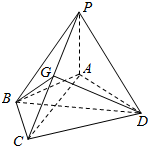 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,G为线段PC上的点,∠ABC=120°
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,$AD=CD=\sqrt{7}$,$PA=\sqrt{3}$,G为线段PC上的点,∠ABC=120°(Ⅰ)证明:BD⊥面PAC;
(Ⅱ)求PC与面PBD所成的角;
(Ⅲ)若G满足PC⊥面GBD,求$\frac{PG}{GC}$的值.
分析 (1)设AC∩BD=O,由△ABD≌△CBD,△ABO≌△CBO,得BD⊥AC,由线面垂直得PA⊥BD,由此能证明BD⊥面PAC.
(2)以O为坐标原点,以OC和OD所在直线为x轴和y轴,建立空间直角坐标系Oxyz,利用向量法能求出PC与面PBD所成角.
(3)设G(x,y,z),$\overrightarrow{CG}=λ\overrightarrow{CP}$,利用向量法能求出$\frac{PG}{GC}$的值.
解答  解:(1)设AC∩BD=O,∵AB=BC=2,$AD=CD=\sqrt{7}$,
解:(1)设AC∩BD=O,∵AB=BC=2,$AD=CD=\sqrt{7}$,
∴△ABD≌△CBD,∴∠ABD=∠CBD,∴△ABO≌△CBO,∴BD⊥AC,
∵PA⊥面ABCD,∴PA⊥BD,
∵PA∩AC=A,∴BD⊥面PAC.
解:(2)以O为坐标原点,以OC和OD所在直线为x轴和y轴,建立空间直角坐标系Oxyz,
P(-$\sqrt{3}$,0,$\sqrt{3}$),B(0,-1,0),D(0,2,0),C($\sqrt{3}$,0,0),
设面PBD的法向量为$\overrightarrow n=(x,y,z)$,
则$\overrightarrow{PB}=(\sqrt{3},-1,-\sqrt{3})$,$\overrightarrow{BD}=(0,3,0)$,$\overrightarrow{PC}=(2\sqrt{3},0,-\sqrt{3})$,
$由\left\{\begin{array}{l}\overrightarrow n⊥\overrightarrow{PB}\\ \overrightarrow n⊥\overrightarrow{BD}\end{array}\right.$,得$\left\{\begin{array}{l}\sqrt{3}x-y-\sqrt{3}z=0\\ 3y=0\end{array}\right.$,取x=1,得$\overrightarrow n=(1,0,1)$,
∴$cos\left?{\overrightarrow{PC},\overrightarrow n}\right>=\frac{{\overrightarrow{PC}•\overrightarrow n}}{{|{\overrightarrow{PC}}|•|{\overrightarrow n}|}}=\frac{{\sqrt{10}}}{10}$,
∴$sinθ=|{cos\left?{\overrightarrow{PC},\overrightarrow n}\right>}|=\frac{{\sqrt{10}}}{10}$,
即PC与面PBD所成角为$arcsin\frac{{\sqrt{10}}}{10}$,
(3)设G(x,y,z),$\overrightarrow{CG}=λ\overrightarrow{CP}$,得$(x-\sqrt{3},y,z)=λ(-2\sqrt{3},0,2\sqrt{3})$
得$\left\{\begin{array}{l}x=\sqrt{3}-2\sqrt{3}λ\\ y=0\\ z=\sqrt{3}λ\end{array}\right.$,即$G(\sqrt{3}-2\sqrt{3}λ,0,\sqrt{3}λ)$,
∴$\overrightarrow{BG}=(\sqrt{3}-2\sqrt{3}λ,1,\sqrt{3}λ)$
由$\overrightarrow{BG}⊥\overrightarrow{PC}$,得$λ=\frac{2}{5}$,即$\frac{PG}{GC}=\frac{3}{2}$.
点评 本题考查线面垂直的证明,考查线面角的求法,考查两线段比值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | (-∞,-$\frac{1}{2}$]∪[1,+∞) | B. | (-∞,-1]∪[1,+∞) | C. | (-∞,-1]∪[0,+∞) | D. | [$\frac{1}{2}$,+∞) |
| A. | ${C}_{8}^{4}$${A}_{4}^{4}$ | B. | ${C}_{8}^{4}$${A}_{4}^{4}$${C}_{5}^{1}$ | C. | 54${C}_{8}^{4}$${A}_{4}^{4}$ | D. | ${C}_{40}^{4}$${A}_{4}^{4}$ |

| A. | 24 | B. | 40 | C. | 36 | D. | 48 |
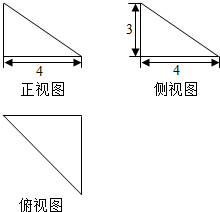 如图为一个几何体的三视图
如图为一个几何体的三视图