题目内容
8．已知棱长为2，各面均为等边三角形的四面体，则其表面积为（ ）| A． | 12 | B． | $2\sqrt{3}$ | C． | $4\sqrt{3}$ | D． | $\frac{4}{3}\sqrt{3}$ |
分析 利用正四面体的结构特征求解．
解答 解：棱长为2，各面均为等边三角形的四面体，
其表面积为：
S=4×（$\frac{1}{2}×2×2×sin60°$）=4$\sqrt{3}$．
故选：C．
点评 本题考查三四面体的表面积的求法，是基础题，解题时要认真审题，注意正四面体的结构特征的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
4．
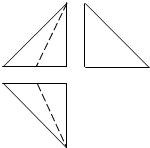如图是一个四面体的三视图，这个三视图均是腰长为2的等腰直角三角形，正视图和俯视图中的虚线是三角形的中线，则该四面体的体积为（ ）
如图是一个四面体的三视图，这个三视图均是腰长为2的等腰直角三角形，正视图和俯视图中的虚线是三角形的中线，则该四面体的体积为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{4}{3}$ | C． | $\frac{8}{3}$ | D． | 2 |
3．若某几何体的三视图如图所示，则此几何体的体积是（ ）
| A． | 24 | B． | 40 | C． | 36 | D． | 48 |
13．某三棱锥的三视图如图所示，则该三棱锥的体积是（ ）
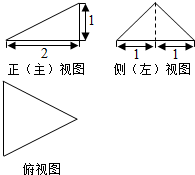
| A． | $\frac{2}{3}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
某商场为推销当地的某种特产进行了一次促销活动，将派出的促销员分成甲、乙两个小组分别在两个不同的场地进行促销，每个小组各6人．以下茎叶图记录了这两个小组成员促销特产的件数，且图中甲组的一个数据已损坏，用x表示，已知甲组促销特产件数的平均数比乙组促销特产件数的平均数少1件．