题目内容
19.已知一个几何体的三视图如图所示,则该几何体的体积为$\frac{32}{3}$.
分析 几何体为正方体与三棱锥的组合体,他们底面相同,高相等.
解答 解:由三视图可知几何体为正方体与三棱锥的组合体,他们底面均是边长为2的正方形,高均为2.
∴V=23+$\frac{1}{3}×{2}^{2}×2$=$\frac{32}{3}$.
故答案为$\frac{32}{3}$.
点评 本题考查了常见几何体的三视图和体积计算,属于基础题.

练习册系列答案
相关题目
10.已知集合M={x|$\frac{1}{x}$≤1},N={x|x2-x-6<0},则M∩N为( )
| A. | {x|-2≤x<0或1<x≤3} | B. | {x|-2<x<0或1≤x<3} | C. | {x|x≤-2或x>3} | D. | {x|x<-2或x≥3} |
7.若曲线y=$\frac{1}{3}$x3+ax2+x存在垂直于y轴的切线,则实数a的取值范围为( )
| A. | (-∞,-$\frac{1}{2}$]∪[1,+∞) | B. | (-∞,-1]∪[1,+∞) | C. | (-∞,-1]∪[0,+∞) | D. | [$\frac{1}{2}$,+∞) |
14.已知平面α和平面β相交,a是α内一条直线,则有( )
| A. | 在β内必存在与a平行的直线 | B. | 在β内必存在与a垂直的直线 | ||
| C. | 在β内不存在与a平行的直线 | D. | 在β内不一定存在与a垂直的直线 |
4.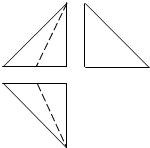 如图是一个四面体的三视图,这个三视图均是腰长为2的等腰直角三角形,正视图和俯视图中的虚线是三角形的中线,则该四面体的体积为( )
如图是一个四面体的三视图,这个三视图均是腰长为2的等腰直角三角形,正视图和俯视图中的虚线是三角形的中线,则该四面体的体积为( )
 如图是一个四面体的三视图,这个三视图均是腰长为2的等腰直角三角形,正视图和俯视图中的虚线是三角形的中线,则该四面体的体积为( )
如图是一个四面体的三视图,这个三视图均是腰长为2的等腰直角三角形,正视图和俯视图中的虚线是三角形的中线,则该四面体的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 2 |
8.某班分成8个小组,每小组5人,现要从中选出4人进行4个不同的化学实验,且每组至多选一人,则不同的安排方法种数是( )
| A. | ${C}_{8}^{4}$${A}_{4}^{4}$ | B. | ${C}_{8}^{4}$${A}_{4}^{4}$${C}_{5}^{1}$ | C. | 54${C}_{8}^{4}$${A}_{4}^{4}$ | D. | ${C}_{40}^{4}$${A}_{4}^{4}$ |
3.若某几何体的三视图如图所示,则此几何体的体积是( )


| A. | 24 | B. | 40 | C. | 36 | D. | 48 |