题目内容
7.抛物线y2=-4px(p>0)的焦点为F,准线为l,则p表示( )| A. | F到l的距离 | B. | F到y轴的距离 | C. | F点的横坐标 | D. | F到l的距离的$\frac{1}{4}$ |
分析 求出抛物线的焦点坐标,即可得出结论.
解答 解:∵抛物线y2=-4px(p>0)的焦点为F,
∴F(-p,0),
∴p表示F到y轴的距离,
故选:B.
点评 本题考查抛物线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.直三棱柱ABC-A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°则此球的表面积等于( )
| A. | $\frac{52π}{9}$ | B. | 20π | C. | 8π | D. | $\frac{52π}{3}$ |
19.设不等式组 $\left\{\begin{array}{l}{x-2y+2≥0}\\{3x-2y-3≤0}\\{x+y-1≥0}\end{array}\right.$,表示的平面区域为D,P(x,y)∈D,若x2+y2≥m恒成立,则实数m的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
16.不等式4x2+4bx+1≤0的解集为∅,则( )
| A. | b<1 | B. | b>-1或b<1 | C. | -1<b<1 | D. | b>1或b<-1 |
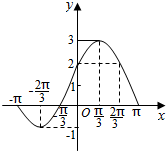 已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.