题目内容
17.直三棱柱ABC-A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°则此球的表面积等于( )| A. | $\frac{52π}{9}$ | B. | 20π | C. | 8π | D. | $\frac{52π}{3}$ |
分析 通过已知条件求出底面外接圆的半径,设此圆圆心为O',球心为O,在RT△OBO'中,求出球的半径,然后求出球的表面积.
解答  解:在△ABC中AB=AC=2,∠BAC=120°,
解:在△ABC中AB=AC=2,∠BAC=120°,
可得BC=2$\sqrt{3}$
由正弦定理,可得△ABC外接圆半径r=2,
设此圆圆心为O',球心为O,在RT△OBO'中,
易得球半径R=$\sqrt{5}$,
故此球的表面积为4πR2=20π
故选:B.
点评 本题是基础题,解题思路是:先求底面外接圆的半径,转化为直角三角形,求出球的半径,这是三棱柱外接球的常用方法;本题考查空间想象能力,计算能力.

练习册系列答案
相关题目
7.用反证法证明“a+b$\sqrt{2}$(a、b∈Z)是无理数”时,假设正确的是( )
| A. | 假设$\sqrt{2}$是有理数 | B. | 假设b$\sqrt{2}$(b∈Z)是有理数 | ||
| C. | 假设a+$\sqrt{2}$(a∈Z)是有理数 | D. | 假设a+b$\sqrt{2}$(a、b∈Z)是有理数 |
12.已知数列{an}的首项a1=2,数列{bn}为等比数列,且${b_n}=\frac{{{a_{n+1}}}}{a_n}$,若b10b11=2,则a21=( )
| A. | 29 | B. | 210 | C. | 211 | D. | 212 |
9.已知函数y=f(x)是定义在上的奇函数,且当x>0时,f(x)=2x-1-3,则f(f(1))=( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
6.一个几何体的三视图如图所示,则该几何体的外接球的体积为( )
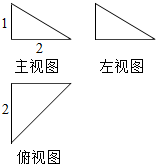

| A. | $\frac{3π}{2}$ | B. | $\frac{9π}{2}$ | C. | $\frac{4π}{3}$ | D. | $\frac{8π}{3}$ |
7.抛物线y2=-4px(p>0)的焦点为F,准线为l,则p表示( )
| A. | F到l的距离 | B. | F到y轴的距离 | C. | F点的横坐标 | D. | F到l的距离的$\frac{1}{4}$ |