题目内容
15.已知等比数列{an}中,a1=2,a4=16.(1)求数列{an}的通项公式an与前n项和Sn;
(2)设等差数列{bn}中,b2=a2,b9=a5,求数列{bn}的通项公式bn与前n项和Sn.
分析 (1)由等比数列前n项和公式求出公比q,由此能求出数列{an}的通项公式an与前n项和Sn.
(2)先求出b2=4,b9=32,再利用等差数列通项公式求出首项和公差,由此能求出数列{bn}的通项公式bn与前n项和Sn.
解答 解:(1)设等比数列{an}的公比为q,
∵a1=2,a4=16,∴16=2q3,解得q=2,
∴${a}_{n}={a}_{1}{q}^{n-1}=2•{2}^{n-1}={2}^{n}$,
${S_n}=\frac{{{a_1}(1-{q^n})}}{1-q}=\frac{{2(1-{2^n})}}{1-2}={2^{n+1}}-2$.
(2)由(1)得b2=a2=4,b9=a5=32,
设等差数列{bn}的公差为d,
则$\left\{\begin{array}{l}{{b}_{1}+d=4}\\{{b}_{1}+8d=32}\end{array}\right.$,解得$\left\{\begin{array}{l}{{b}_{1}=0}\\{d=4}\end{array}\right.$,
∴bn=4n-4,
∴${S}_{n}={b}_{1}n+\frac{n(n-1)}{2}d$=$\frac{n(n-1)}{2}×4$=2n2-2n.
点评 本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要注意等差数列和等比数列的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.一个几何体的三视图如图所示,则该几何体的外接球的体积为( )
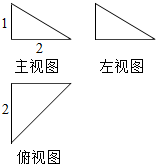

| A. | $\frac{3π}{2}$ | B. | $\frac{9π}{2}$ | C. | $\frac{4π}{3}$ | D. | $\frac{8π}{3}$ |
3.已知直线y=x+1交椭圆${x^2}+\frac{y^2}{2}=1$于A、B两点,则弦AB的长为( )
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $\sqrt{2}$ |
7.抛物线y2=-4px(p>0)的焦点为F,准线为l,则p表示( )
| A. | F到l的距离 | B. | F到y轴的距离 | C. | F点的横坐标 | D. | F到l的距离的$\frac{1}{4}$ |