题目内容
已知函数f(x)=|x+1|+|x-1|;
(1)分别写出当x∈(-∞,-1)、x∈(-1,1)、x∈(1,+∞)时的函数解析式;
(2)将函数f(x)=|x+1|+|x-1|写成分段函数;
(3)画出函数的图象.
(1)分别写出当x∈(-∞,-1)、x∈(-1,1)、x∈(1,+∞)时的函数解析式;
(2)将函数f(x)=|x+1|+|x-1|写成分段函数;
(3)画出函数的图象.
考点:函数的图象,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:根据分段函数的定义去掉绝对值是解决本题的关键.利用分类讨论思想确定出各段的函数类型,选择关键点或者相应函数的图象确定要素准确画出该函数的图象.
解答:
 解:(1)当x∈(-∞,-1)时,f(x)=-2x、
解:(1)当x∈(-∞,-1)时,f(x)=-2x、
当x∈(-1,1)时,f(x)=2,
当x∈(1,+∞)时,f(x)=2x;
(2)f(x)=|x+1|+|x-1|=
,
(3)图象如图所示,
 解:(1)当x∈(-∞,-1)时,f(x)=-2x、
解:(1)当x∈(-∞,-1)时,f(x)=-2x、当x∈(-1,1)时,f(x)=2,
当x∈(1,+∞)时,f(x)=2x;
(2)f(x)=|x+1|+|x-1|=
|
(3)图象如图所示,
点评:本题主要考查函数的图象和性质应用,体现了分类讨论、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=
,则下列结论正确的是( )
|
| A、f(x)是偶函数 |
| B、f(x)是增函数 |
| C、f(x)的值域为[-1,+∞) |
| D、f(x)是周期函数 |
从正六边形六个顶点及其中心这7个点中,任取两个点,则这两个点的距离大于该正六边形边长的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
抛物线x2+y=0的焦点坐标是( )
A、(0,-
| ||
B、(0,
| ||
C、(
| ||
D、(-
|
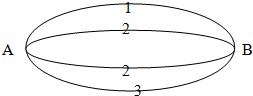 如图A、B两点之间有4条网线并联,他们能通过的最大信息量分别为1、2、2、3,现从中任取三条网线且使每条网线通过最大信息量;
如图A、B两点之间有4条网线并联,他们能通过的最大信息量分别为1、2、2、3,现从中任取三条网线且使每条网线通过最大信息量;