题目内容
6.f(x)=4x2-mx+5在区间[-2,+∞)上是增函数,求m的范围m≤-16.分析 求出二次函数的对称轴,然后求解即可.
解答 解:f(x)=4x2-mx+5的开口向上,对称轴为:x=$\frac{m}{8}$,f(x)=4x2-mx+5在区间[-2,+∞)上是增函数,
可得:$\frac{m}{8}≤-2$,解得m≤-16.
故答案为:m≤-16
点评 本题考查二次函数的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
18.已知集合A={x|ax2+x-3=0},B={x|3≤x<7},若A∩B≠∅,则实数a的取值集合为( )
| A. | $[-\frac{1}{12},-\frac{4}{49})$ | B. | $[-\frac{1}{12},0]$ | C. | $(-\frac{4}{49},0]$ | D. | $[-\frac{4}{49},0]$ |
15.已知x,y为正实数,且x+y+$\frac{1}{x}$+$\frac{1}{y}$=5,则x+y的最大值是( )
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
16.过抛物线y=2x2的焦点F作倾斜角为120°的直线交抛物线于A、B两点,则弦|AB|的长为( )
| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
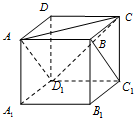 在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动,则下列四个命题:
在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动,则下列四个命题: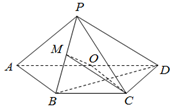 如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.