题目内容
11.设偶函数f(x)对任意x∈R,都有$f(x+3)=-\frac{1}{f(x)}$,且当x∈[-3,-2]时,f(x)=4x,则f(2018)=-8.分析 由已知得f(x+6)=-$\frac{1}{f(x+3)}$=f(x),从而当x∈[2,3]时,f(x)=f(-x),进而得到f(2018)=f(2)=f(-2),由此能求出结果.
解答 解:∵偶函数f(x)对任意x∈R,都有$f(x+3)=-\frac{1}{f(x)}$,
∴f(x+6)=-$\frac{1}{f(x+3)}$=f(x),
∵当x∈[-3,-2]时,f(x)=4x,
∴当x∈[2,3]时,f(x)=f(-x),
∴f(2018)=f(2)=f(-2)=4×(-2)=-8.
故答案为:-8.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
16.若复数z满足zi=2-3i(i是虚数单位),则复数z的共轭复数为( )
| A. | -3-2i | B. | -3+2i | C. | 2+3i | D. | 3-2i |
20.复数$z=\frac{-2+2i}{1+i}$的共轭复数是( )
| A. | 1+i | B. | 1-i | C. | 2i | D. | -2i |
1.已知α∈(0,π),若sinα+cosα=$\frac{\sqrt{3}}{3}$,则cos2α-sin2α=( )
| A. | -$\frac{\sqrt{5}}{3}$ | B. | -$\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
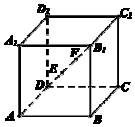 如图,在正方体ABCD-A1B1C1D1中,AB=3$\sqrt{3}$,点E,F在线段DB1上,且DE=EF=FB1,点M是正方体表面上的一动点,点P,Q是空间两动点,若$\frac{|PE|}{|PF|}$=$\frac{|QE|}{|QF|}$=2且|PQ|=4,则$\overrightarrow{MP}$•$\overrightarrow{MQ}$的最小值为-$\frac{8}{3}$.
如图,在正方体ABCD-A1B1C1D1中,AB=3$\sqrt{3}$,点E,F在线段DB1上,且DE=EF=FB1,点M是正方体表面上的一动点,点P,Q是空间两动点,若$\frac{|PE|}{|PF|}$=$\frac{|QE|}{|QF|}$=2且|PQ|=4,则$\overrightarrow{MP}$•$\overrightarrow{MQ}$的最小值为-$\frac{8}{3}$.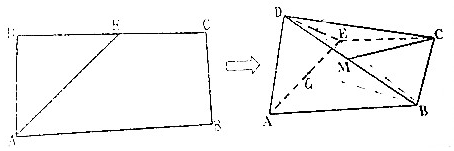
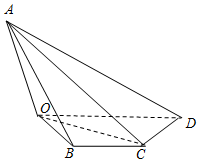 如图,四棱锥A-OBCD中,已知平面AOC⊥面OBCD,AO=2$\sqrt{3}$,OB=BC=2,CD=4,∠OBC=∠BCD=120°.
如图,四棱锥A-OBCD中,已知平面AOC⊥面OBCD,AO=2$\sqrt{3}$,OB=BC=2,CD=4,∠OBC=∠BCD=120°.