题目内容
1.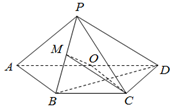 如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点.(Ⅰ)求证:PD∥平面OCM;
(Ⅱ)若AP与平面PBD所成的角为60°,求线段PB的长.
分析 (Ⅰ)连接BD交OC与N,连接MN.证明MN∥PD.然后证明PD∥平面OCM.
(Ⅱ)通过计算证明AB⊥BD.AB⊥PD.推出AB⊥平面BDP,说明∠APB为AP与平面PBD所成的角,然后求解即可.
解答  (本小题满分15分)
(本小题满分15分)
解:(Ⅰ)连接BD交OC与N,连接MN.
因为O为AD的中点,AD=2,
所以OA=OD=1=BC.
又因为AD∥BC,
所以四边形OBCD为平行四边形,…(2分)
所以N为BD的中点,因为M为PB的中点,
所以MN∥PD.…(4分)
又因为MN?平面OCM,PD?平面OCM,
所以PD∥平面OCM.…(6分)
(Ⅱ)由四边形OBCD为平行四边形,知OB=CD=1,
所以△AOB为等边三角形,所以∠A=60°,…(8分)
所以$BD=\sqrt{1+4-2×1×2×\frac{1}{2}}=\sqrt{3}$,即AB2+BD2=AD2,即AB⊥BD.
因为DP⊥平面ABP,所以AB⊥PD.
又因为BD∩PD=D,所以AB⊥平面BDP,…(11分)
所以∠APB为AP与平面PBD所成的角,即∠APB=60°,…(13分)
所以$PB=\frac{{\sqrt{3}}}{3}$. …(15分)
点评 本题考查直线与平面垂直的判定定理以及性质定理的应用,直线与平面所成角的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
12.已知定义在R上的函数f(x)为周期函数,且周期为4,若在区间[-2,2]上,f(x)=$\left\{\begin{array}{l}{{2}^{x}+2m,-2≤x≤0}\\{lo{g}_{2}x-m,0<x≤2}\end{array}\right.$,则f(2017m)=( )
| A. | -$\frac{9}{4}$ | B. | -$\frac{5}{2}$ | C. | $\frac{9}{4}$ | D. | $\frac{5}{2}$ |
9.以下函数中在区间(0,+∞)上单调递增的函数是( )
| A. | y=|x|+1 | B. | y=$\frac{1}{x}$ | C. | y=-x2+1 | D. | y=-x|x| |
13.抛物线x=4y2的焦点坐标是( )
| A. | (0,1) | B. | (0,-1) | C. | $({-\frac{1}{16},0})$ | D. | $({\frac{1}{16},0})$ |
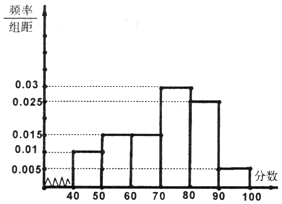 某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题: