题目内容
14.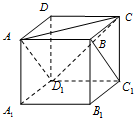 在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动,则下列四个命题:
在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动,则下列四个命题:①三棱锥A-D1PC的体积不变;
②直线AP与平面ACD1所成的角的大小不变;
③二面角P-AD1-C的大小不变;
④M是平面A1B1C1D1上到点D和C1距离相等的点,则M点的轨迹是直线A1D1.
其中真命题的编号是①③④(写出所有真命题的编号)
分析 ①:点P是直线BC1的动点,△AD1P的面积是定值,而点C到平面AD1P的距离也是定值,故得到结论;
②:可以从向量的角度进行判断;
③:平面PD1A平面ACD1的法向量的夹角是不变的,得到结论.
④:由M是平面A1B1C1D1上到点D和C1距离相等的点,M点的轨迹是线段DC1在空间的垂直平分线与面A1B1C1D1的交点.
解答 解:对于①:∵点P是直线BC1的动点,∴△AD1P的面积是定值,∵点C到平面AD1P的距离不变,∴①正确;
对于②:∵随着P点的移动,$\overrightarrow{AP}$与平面ACD1的法向量的夹角也是变化的,∴②错误;
对于③:∵平面PD1A平面ACD1的法向量的夹角是不变的,∴③正确;
对于④:∵M是平面A1B1C1D1上到点D和C1距离相等的点,∴M点的轨迹是线段DC1在空间的垂直平分线与面A1B1C1D1的交点,故其轨迹是直线A1D1,故④正确.
故答案为,①③④
点评 本题考查了空间点、线、面的位置关系,空间轨迹问题,属于中档题.

练习册系列答案
相关题目
1.已知函数$f(x)=\left\{\begin{array}{l}{x^2}-2x,x≤0\\ \frac{{\sqrt{x}}}{e^x},x>0\end{array}\right.$,若关于x的方程f(x)-a+1=0恰有3个不同的实数根,则实数a的取值范围为( )
| A. | $(1,\frac{{\sqrt{2e}}}{2e}+1)$ | B. | $(1,\frac{1}{e}+1)$ | C. | $(0,\frac{1}{2e}+1)$ | D. | $(\frac{1}{e},1)$ |
9.以下函数中在区间(0,+∞)上单调递增的函数是( )
| A. | y=|x|+1 | B. | y=$\frac{1}{x}$ | C. | y=-x2+1 | D. | y=-x|x| |
4.已知过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F作倾斜角120°的直线l交椭圆为A,B,若$\overrightarrow{AF}$=2$\overrightarrow{FB}$,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2}{3}$ |
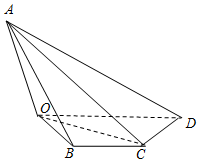 如图,四棱锥A-OBCD中,已知平面AOC⊥面OBCD,AO=2$\sqrt{3}$,OB=BC=2,CD=4,∠OBC=∠BCD=120°.
如图,四棱锥A-OBCD中,已知平面AOC⊥面OBCD,AO=2$\sqrt{3}$,OB=BC=2,CD=4,∠OBC=∠BCD=120°.