题目内容
在△ABC中,a=2,A=45°,若此三角形有两解,则b的范围为( )
A、2<b<2
| ||||
| B、b>2 | ||||
| C、b<2 | ||||
D、
|
考点:正弦定理
专题:解三角形
分析:利用正弦定理列出关系式,把a,sinA的值代入,表示出b,B+C,根据B为两值,得到两个值互补,确定出B的范围,进而求出sinB的范围,即可确定出b的范围.
解答:
解:∵在△ABC中,a=2,A=45°,且此三角形有两解,
∴由正弦定理
=
=2
,
∴b=2
sinB,B+C=180°-45°=135°,
由B有两个值,得到这两个值互补,
若B≤45°,则和B互补的角大于等于135°,这样A+B≥180°,不成立;
∴45°<B<135°,
又若B=90,这样补角也是90°,一解,
∴
<sinB<1,b=2
sinB,
则2<b<2
,
故选:A.
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| 2 |
∴b=2
| 2 |
由B有两个值,得到这两个值互补,
若B≤45°,则和B互补的角大于等于135°,这样A+B≥180°,不成立;
∴45°<B<135°,
又若B=90,这样补角也是90°,一解,
∴
| ||
| 2 |
| 2 |
则2<b<2
| 2 |
故选:A.
点评:此题考查了正弦、余弦定理,熟练掌握定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知log2m=2.013,log2n=1.013,则
等于( )
| n |
| m |
| A、2 | ||
B、
| ||
| C、10 | ||
D、
|
在锐角△ABC中,角A、B、C所对应的边分别为a,b,c,若b=2asinB,则角A等于( )
| A、30° | B、45° |
| C、60° | D、75° |
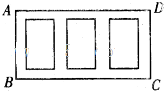 如图,某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的小矩形绿化区,这三块绿化区四周和绿化区之间分别设有2米宽和1米宽的走道,已知三块绿化区的总面积为600平方米,求该矩形区域ABCD占地面积的最小值.
如图,某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的小矩形绿化区,这三块绿化区四周和绿化区之间分别设有2米宽和1米宽的走道,已知三块绿化区的总面积为600平方米,求该矩形区域ABCD占地面积的最小值.