题目内容
给出四个命题
(1)函数是定义域到值域的对应关系.
(2)函数f(x)=
+
.
(3)f(x)=5,因为这个函数的值不随x的变化而变化.所以f(t2+1)=5.
(4)y=2x(x∈N)的图象是一条直线.
其中正确的是 .
(1)函数是定义域到值域的对应关系.
(2)函数f(x)=
| x-4 |
| 3-x |
(3)f(x)=5,因为这个函数的值不随x的变化而变化.所以f(t2+1)=5.
(4)y=2x(x∈N)的图象是一条直线.
其中正确的是
考点:函数的概念及其构成要素
专题:函数的性质及应用
分析:根据函数的定义和性质分别进行判断即可.
解答:
解:(1)根据函数的三要素可知,函数是定义域到值域的对应关系.正确.
(2)要使函数有意义,则
,即
,此时无解,即定义域为空集,不满足函数的定义,故f(x)=
+
为函数,错误.
(3)∵f(x)=5为常数函数,故这个函数的值不随x的变化而变化.所以f(t2+1)=5.正确.
(4)y=2x(x∈N)的图象不连续,不是一条直线.故错误,
故答案为:(1)(3)
(2)要使函数有意义,则
|
|
| x-4 |
| 3-x |
(3)∵f(x)=5为常数函数,故这个函数的值不随x的变化而变化.所以f(t2+1)=5.正确.
(4)y=2x(x∈N)的图象不连续,不是一条直线.故错误,
故答案为:(1)(3)
点评:本题主要考查函数定义的理解和应用,根据函数的三要素以及定义是解决本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
在△ABC中,a=2,A=45°,若此三角形有两解,则b的范围为( )
A、2<b<2
| ||||
| B、b>2 | ||||
| C、b<2 | ||||
D、
|
若f(lgx)=x,则f(3)=( )
| A、103 |
| B、3 |
| C、lg3 |
| D、310 |
下列四组中的函数f(x)与g(x),是同一函数的是( )
| A、f(x)=ln(1-x)+ln(1+x),g(x)=ln(1-x2) | ||||||
| B、f(x)=lgx2,g(x)=2lgx | ||||||
C、f(x)=
| ||||||
D、f(x)=
|
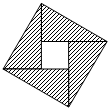 三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示,我们教材中利用该图作为“( )”的几何解释.
三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示,我们教材中利用该图作为“( )”的几何解释.| A、如果a>b,b>c,那么a>c |
| B、如果a>b>0,那么a2>b2 |
| C、对任意实数a和b,有a2+b2≥2ab,当且仅当a=b时等号成立 |
| D、如果a>b,c>0那么ac>bc |
在(x+y)n的展开式中,若第8项系数最大,则n的值可能等于( )
| A、14,15 |
| B、15,16 |
| C、16,17 |
| D、14,15,16 |
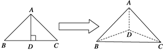 如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,则下列四个结论中错误的是( )
如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,则下列四个结论中错误的是( )| A、BD⊥AC | ||
| B、△ABC是等边三角形 | ||
| C、平面ADC⊥平面ABC | ||
D、二面角A-BC-D的正切值为
|