题目内容
已知数列{an}的前n项和为Sn,且2Sn=3an-1,等差数列{bn}中,b2+b5=12,b3+b8=20,设数列{bn}的前n项和为Tn,比较an与Tn的大小.
考点:数列的求和
专题:等差数列与等比数列
分析:2Sn=3an-1,当n≥2时,2Sn-1=3an-1-1;两式相减可得an=3an-1.利用等比数列的通项公式可得an=3n-1.
设等差数列{bn}的公差为d,由于b2+b5=12,b3+b8=20,bn=2n-1.可得Tn=n2.对n分类讨论即可比较出其大小.
设等差数列{bn}的公差为d,由于b2+b5=12,b3+b8=20,bn=2n-1.可得Tn=n2.对n分类讨论即可比较出其大小.
解答:
解:∵2Sn=3an-1,当n≥2时,2Sn-1=3an-1-1;
两式相减可得:2an=3an-3an-1,化为an=3an-1.
当n=1时,2a1=3a1-1,解得a1=1.
∴数列{an}是等比数列,
an=3n-1.
设等差数列{bn}的公差为d,
∵b2+b5=12,b3+b8=20,
∴b1+d+b1+4d=12,b1+2d+b1+7d=20,
解得b1=1,d=2.
∴bn=1+2(n-1)=2n-1.
∴Tn=
=n2.
当n=1时,a1=T1=1;
当n=2时,a2=3<T2=4;
当n=3时,a3=9=T3;
当n≥4时,(1+2)n=1+
•2+
•22+
•23+…
=1+2n+2n(n-1)+
+…
>3n2,
∴an>Tn.
综上可得:当n=1或3时,an=Tn;
当n=2时,a2<T2;
当n≥4时,an>Tn.
两式相减可得:2an=3an-3an-1,化为an=3an-1.
当n=1时,2a1=3a1-1,解得a1=1.
∴数列{an}是等比数列,
an=3n-1.
设等差数列{bn}的公差为d,
∵b2+b5=12,b3+b8=20,
∴b1+d+b1+4d=12,b1+2d+b1+7d=20,
解得b1=1,d=2.
∴bn=1+2(n-1)=2n-1.
∴Tn=
| n(1+2n-1) |
| 2 |
当n=1时,a1=T1=1;
当n=2时,a2=3<T2=4;
当n=3时,a3=9=T3;
当n≥4时,(1+2)n=1+
| ∁ | 1 n |
| ∁ | 2 n |
| ∁ | 3 n |
=1+2n+2n(n-1)+
| 4n(n-1)(n-2) |
| 3 |
>3n2,
∴an>Tn.
综上可得:当n=1或3时,an=Tn;
当n=2时,a2<T2;
当n≥4时,an>Tn.
点评:本题考查了递推式的应用、等差数列与等比数列的通项公式及其前n项和公式、二项式定理的应用,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
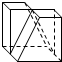
某几何体的立体图如图所示,该几何体的三视图不可能是( )

A、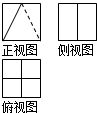 |
B、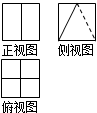 |
C、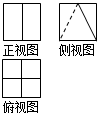 |
D、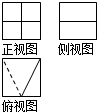 |
过椭圆
+
=1上一点M(0,2)作圆x2+y2=2的两条切线,点A,B为切点,O为坐标原点,则△AOB的面积为( )
| x2 |
| 9 |
| y2 |
| 4 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
设α∈(0,π),且tanα=
,则cosα=( )
| 5 |
| A、2 | ||||
B、-
| ||||
C、
| ||||
D、
|
函数f(x)=log2(x+a)的图象过一、二、三象限,则a的取值范围是( )
| A、a>1 | B、a≥1 |
| C、a<-1 | D、a≤-1 |