题目内容
下列说法中错误的命题是 ．
①一个命题的逆命题为真，它的否命题也一定为真；
②命题“?x∈R，x2-x≤0”的否定是“?x∈R，x2-x≥0”；
③“矩形的两条对角线相等”的逆命题是真命题；
④“x≠3”是“|x|≠3”成立的充分条件．
①一个命题的逆命题为真，它的否命题也一定为真；
②命题“?x∈R，x2-x≤0”的否定是“?x∈R，x2-x≥0”；
③“矩形的两条对角线相等”的逆命题是真命题；
④“x≠3”是“|x|≠3”成立的充分条件．
考点：命题的真假判断与应用
专题：简易逻辑
分析：根据一个命题的逆命题和否命题互为逆否命题，真假性相同，可判断①；写出原命题的否定，可判断②；写出原命题的逆命题，可判断③；写出“若x≠3，则|x|≠3”的逆否命题并判断真，进而根据充要条件的定义，可判断④．
解答：
解：一个命题的逆命题和否命题互为逆否命题，真假性相同，故①正确；
命题“?x∈R，x2-x≤0”的否定是“?x∈R，x2-x＞0”，故②错误；
“矩形的两条对角线相等”的逆命题是“两条对角线相等的图形是矩形”为假命题，故③错误；
“若x≠3，则|x|≠3”的逆否命题为：若“|x|=3，则x=3”，为假命题，
故“若x≠3，则|x|≠3”不成立，故“x≠3”不是“|x|≠3”成立的充分条件，故④错误；
故答案为：②③④
命题“?x∈R，x2-x≤0”的否定是“?x∈R，x2-x＞0”，故②错误；
“矩形的两条对角线相等”的逆命题是“两条对角线相等的图形是矩形”为假命题，故③错误；
“若x≠3，则|x|≠3”的逆否命题为：若“|x|=3，则x=3”，为假命题，
故“若x≠3，则|x|≠3”不成立，故“x≠3”不是“|x|≠3”成立的充分条件，故④错误；
故答案为：②③④
点评：本题以命题的真假判断为载体考查了四种命题，充要条件，命题的否定等知识点，是简单逻辑的综合应用，难度不大，属于基础题．
练习册系列答案
相关题目
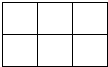某农场有如图所示的2行3列共六块土地，现有萝卜、玉米、油菜三类蔬菜可种．要求每块土地种一类蔬菜，每类蔬菜种两块土地，每行的蔬菜种类各不相同，则恰有一类蔬菜种在同列的种植方法数为