题目内容
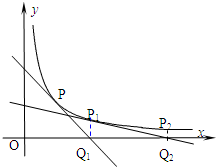 如图,已知曲线C:y=
如图,已知曲线C:y=| 1 |
| x |
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)求证:三角形PnPn+1Pn+2的面积为定值.
考点:数列的应用,利用导数研究曲线上某点切线方程
专题:综合题,等差数列与等比数列
分析:(Ⅰ)通过求导即可得到切线的斜率,进而得到切线的方程,即可得到xn+1与xn的关系,利用等比数列的通项公式即可求出.
(Ⅱ)求出SPnQnQnPn+1=
(
+
)(2n+1-2n)=
,SPn+1Qn+1Qn+1Pn+2=
,SPnQnQn+2Pn+2=
,即可求出三角形PnPn+1Pn+2的面积为定值.
(Ⅱ)求出SPnQnQnPn+1=
| 1 |
| 2 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 15 |
| 8 |
解答:
解:(Ⅰ)由y=
求导得y′=-
,
∴曲线C:y=
在点P(1,1)处的切线方程为y-1=-(x-1),即y=-x+2.
此切线与x轴的交点Q1的坐标为(2,0),
∴点P1的坐标为(2,
).即x1=2,y1=
.-------------------(2分)
∵点Pn的坐标为(xn,yn)(n∈N*),Pn在曲线C上,所以yn=
,
∴曲线C:y=
在点Pn(xn,yn)处的切线方程为y-
=-
(x-xn),---(5分)
令y=0,得点Qn+1的横坐标为xn+1=2xn.
∴数列{xn}是以2为首项,2为公比的等比数列.
∴xn=2n(n∈N*).---------------------(8分)
(Ⅱ)设Pn(xn,yn),Pn+1(xn+1,yn+1),Pn+2(xn+2,yn+2),
∵SPnQnQnPn+1=
(
+
)(2n+1-2n)=
,SPn+1Qn+1Qn+1Pn+2=
,SPnQnQn+2Pn+2=
,
∴△PnPn+1Pn+2的面积为
-
-
=
.
| 1 |
| x |
| 1 |
| x2 |
∴曲线C:y=
| 1 |
| x |
此切线与x轴的交点Q1的坐标为(2,0),
∴点P1的坐标为(2,
| 1 |
| 2 |
| 1 |
| 2 |
∵点Pn的坐标为(xn,yn)(n∈N*),Pn在曲线C上,所以yn=
| 1 |
| xn |
∴曲线C:y=
| 1 |
| x |
| 1 |
| xn |
| 1 | ||
|
令y=0,得点Qn+1的横坐标为xn+1=2xn.
∴数列{xn}是以2为首项,2为公比的等比数列.
∴xn=2n(n∈N*).---------------------(8分)
(Ⅱ)设Pn(xn,yn),Pn+1(xn+1,yn+1),Pn+2(xn+2,yn+2),
∵SPnQnQnPn+1=
| 1 |
| 2 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 15 |
| 8 |
∴△PnPn+1Pn+2的面积为
| 15 |
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
点评:熟练掌握导数的几何意义、等比数列的通项公式及其前n项和公式,三角形面积计算公式是关键.

练习册系列答案
相关题目
已知函数f(x)=
的定义域为R,则实数m取值范围为( )
| -mx2+6mx-m+8 |
| A、{m|-1≤m≤0} |
| B、{m|-1<m<0} |
| C、{m|m≤0} |
| D、{m|m<-1或m>0} |
已知函数f(x)=
+
ax2+2bx+c的两个极值分别为f(x1)和f(x2),若x1和x2分别在区间(-2,0)与(0,2)内,则
的取值范围为( )
| x3 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
A、(-2,
| ||
B、[-2,
| ||
C、(-∞,-2)∪(
| ||
D、(-∞,-2]∪[
|
已知a,b为非零实数,且a<b,则下列不等式成立的是( )
| A、a2<b2 | ||||
| B、|a|<|b| | ||||
C、
| ||||
D、
|
 如图所示:m个实数a1,a2,…,am,(m≥3,m∈N)依次按顺时针方向围成一个圆圈.
如图所示:m个实数a1,a2,…,am,(m≥3,m∈N)依次按顺时针方向围成一个圆圈. 如图,已知四棱锥P-ABCD的底面ABCD是菱形,PA⊥平面ABCD,点F为PC的中点.
如图,已知四棱锥P-ABCD的底面ABCD是菱形,PA⊥平面ABCD,点F为PC的中点.