题目内容
已知a,b为非零实数,且a<b,则下列不等式成立的是( )
| A、a2<b2 | ||||
| B、|a|<|b| | ||||
C、
| ||||
D、
|
考点:不等式的基本性质
专题:不等式的解法及应用
分析:取a=-2,b=-1,满足a<b,即可排除A,B,D.利用不等式的基本性质即可判断出C.
解答:
解:对于A.取a=-2,b=-1,满足a<b,但是a2<b2不成立;
对于B.取a=-2,b=-1,满足a<b,但是|a|<|b|不成立;
对于C.∵a,b为非零实数,且a<b,∴
<0,化为
<
,正确;
对于D.取a=-2,b=-1,则
=2>1,因此不正确.
综上可得:只有C正确.
故选:C.
对于B.取a=-2,b=-1,满足a<b,但是|a|<|b|不成立;
对于C.∵a,b为非零实数,且a<b,∴
| a-b |
| a2b2 |
| 1 |
| ab2 |
| 1 |
| a2b |
对于D.取a=-2,b=-1,则
| a |
| b |
综上可得:只有C正确.
故选:C.
点评:本题考查了取特殊值否定一个命题的方法,考查了不等式的基本性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式x2-x-2>0的解集为( )
| A、(-1,2) |
| B、(-∞,-1)∪(2,+∞) |
| C、(-1,2] |
| D、(-1,2) |
函数f(x)=sin2x的导数是( )
| A、2sinx |
| B、2cosx |
| C、2sin2x |
| D、sin2x |
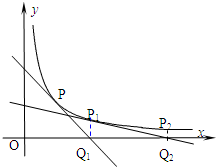 如图,已知曲线C:y=
如图,已知曲线C:y=