题目内容
已知函数f(x)=esinx+cosx-
sin2x(x∈R),则函数f(x)的最大值与最小值的差是 .
| 1 |
| 2 |
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:令t=sinx+cosx=
sin(x+
),则t∈[-
,
],且sin2x=t2-1,利用导数法分析y=et-
(t2-1)在[-
,
]上单调性,进而可得答案.
| 2 |
| π |
| 4 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
解答:
解:令t=sinx+cosx=
sin(x+
),则t∈[-
,
],
且sin2x=t2-1,
则y=f(x)=et-
(t2-1),
∵y′=et-t>0在t∈[-
,
]时恒成立,
故y=et-
(t2-1)在[-
,
]上为增函数,
故函数f(x)的最大值与最小值的差是y| t=
-y| t=-
=(e
-
)-(e-
-
)=e
-e-
,
故答案为:e
-e-
| 2 |
| π |
| 4 |
| 2 |
| 2 |
且sin2x=t2-1,
则y=f(x)=et-
| 1 |
| 2 |
∵y′=et-t>0在t∈[-
| 2 |
| 2 |
故y=et-
| 1 |
| 2 |
| 2 |
| 2 |
故函数f(x)的最大值与最小值的差是y| t=
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:e
| 2 |
| 2 |
点评:本题主要考查函数求最值,常要借助函数的单调性,因为本题构成比较复杂,所以采用换元法简化函数的解析式.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
直线kx-y+1=0与圆(x-1)2+y2=4的位置关系是( )
| A、相交 | B、相切 |
| C、相离 | D、不确定,与k有关 |
满足{1}⊆M⊆{1,2,3,4,5}的集合M的个数为( )
| A、4 | B、6 | C、8 | D、16 |
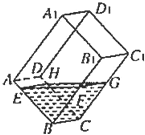 如图,在透明材料制成的长方体容器ABCD-A1B1C1D1内灌注一些水,固定容器底面一边BC于桌面上,再将容器倾斜根据倾斜度的不同,有下列命题:
如图,在透明材料制成的长方体容器ABCD-A1B1C1D1内灌注一些水,固定容器底面一边BC于桌面上,再将容器倾斜根据倾斜度的不同,有下列命题: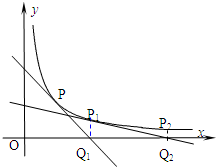 如图,已知曲线C:y=
如图,已知曲线C:y=