题目内容
已知函数f（x）=
的定义域为R，则实数m取值范围为（ ）
| -mx2+6mx-m+8 |
| A、{m|-1≤m≤0} |
| B、{m|-1＜m＜0} |
| C、{m|m≤0} |
| D、{m|m＜-1或m＞0} |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：本题对根号内函数可分类讨论，分为二次函数和非二次函数，当二次函数值非负时，可利用对应方程根的判别式满足的关系，解得本题结论．
解答：
解：∵函数f（x）=
的定义域为R，
∴函数y=-mx2+6mx-m+8的函数值非负，
（1）当m=0时，y=8，函数值非负，适合题意；
（2）当m≠0时，关于x的方程-mx2+6mx-m+8=0根的判别式△≤0，
即（6m）2-4（-m）（-m+8）≤0，m2+m≤0，-1≤m≤0，
∴-1＜m≤0
综上，-1≤m≤0．
故选：A．
| -mx2+6mx-m+8 |
∴函数y=-mx2+6mx-m+8的函数值非负，
（1）当m=0时，y=8，函数值非负，适合题意；
（2）当m≠0时，关于x的方程-mx2+6mx-m+8=0根的判别式△≤0，
即（6m）2-4（-m）（-m+8）≤0，m2+m≤0，-1≤m≤0，
∴-1＜m≤0
综上，-1≤m≤0．
故选：A．
点评：本题考查的是函数定义域、二次函数的图象、不等式的知识，还考查了分类讨论的数学思想，本题难度不大，属于基础题．
练习册系列答案
精英口算卡系列答案
相关题目
直线kx-y+1=0与圆（x-1）2+y2=4的位置关系是（ ）
| A、相交 | B、相切 |
| C、相离 | D、不确定，与k有关 |
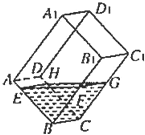如图，在透明材料制成的长方体容器ABCD-A1B1C1D1内灌注一些水，固定容器底面一边BC于桌面上，再将容器倾斜根据倾斜度的不同，有下列命题：
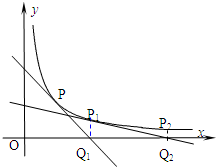如图，已知曲线C：y=