题目内容
求函数y=cos2x-cosx-
,x∈[
,π]的值域.
| 11 |
| 4 |
| π |
| 3 |
考点:三角函数的最值
专题:三角函数的求值
分析:由题意可得cosx∈[-1,
],函数y=cos2x-cosx-
=(cosx-
)2-3,再利用二次函数的性质,求得函数的值域.
| 1 |
| 2 |
| 11 |
| 4 |
| 1 |
| 2 |
解答:
解:由x∈[
,π]可得 cosx∈[-1,
],由于函数y=cos2x-cosx-
=(cosx-
)2-3,
故当cosx=
时,函数y取得最小值为3;当cosx=-1时,函数y取得最大值为-
,故函数y的值域为[-3,-
].
| π |
| 3 |
| 1 |
| 2 |
| 11 |
| 4 |
| 1 |
| 2 |
故当cosx=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题主要考查余弦函数的定义域和值域,二次函数的性质,属于基础题.

练习册系列答案
相关题目
函数f(x)=sin2x的导数是( )
| A、2sinx |
| B、2cosx |
| C、2sin2x |
| D、sin2x |
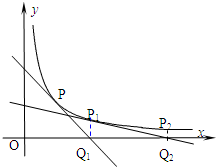 如图,已知曲线C:y=
如图,已知曲线C:y=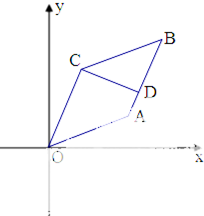 如图,在平行四边形OABC中,已知点A(3,1),C(1,3).
如图,在平行四边形OABC中,已知点A(3,1),C(1,3).