题目内容
设函数f(x)=b•ln(x+1)+x2其中b≠0.
(1)若函数f(x)在定义域上单调递增,求b的取值范围;
(2)若函数f(x)有极值点,写出b的取值范围及函数f(x)的极值点;
(3)证明对任意的正整数n,不等式ln(
+1)>
-
成立.
(1)若函数f(x)在定义域上单调递增,求b的取值范围;
(2)若函数f(x)有极值点,写出b的取值范围及函数f(x)的极值点;
(3)证明对任意的正整数n,不等式ln(
| 1 |
| n |
| 1 |
| n2 |
| 1 |
| n3 |
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)由f′(x)=
,令g(x)=2x2+2x+b,则g(x)在(-
,+∞)上递增,在(-1,-
)上递减,从而g(x)min=g(-
)=-
+b,当b>
时,g(x)min=-
+b>0,进而求出b的范围,
(2)由(1)知当b>
时函数f(x)无极值点,再分别讨论当b=
时,当b<
时的范围,从而求出函数的极值点,
(3)当b=-1时,f(x)=x2-ln(x+1).令h(x)=x3-x2+ln(x+1),由h(x)=
在[0,+∞)上恒正,得恒有h(x)>h(0)=0即当x∈(0,+∞)时,有x3-x2+ln(x+1)>0,ln(x+1)>x2-x3,对任意正整数n,取x=
得ln(
+1)>
-
.
| 2x2+2x+b |
| x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)知当b>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)当b=-1时,f(x)=x2-ln(x+1).令h(x)=x3-x2+ln(x+1),由h(x)=
| 3x3+(x-1)2 |
| x+1 |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n2 |
| 1 |
| n3 |
解答:
解:(1)函数f(x)=x2+bln(x+1)的定义域在(-1,+∞),
由f′(x)=
,
令g(x)=2x2+2x+b,
则g(x)在(-
,+∞)上递增,在(-1,-
)上递减,
∴g(x)min=g(-
)=-
+b,
当b>
时,g(x)min=-
+b>0,
g(x)=2x2+2x+b>0在(-1,+∞)上恒成立,
所以f'(x)>0即当b>
时,函数f(x)在定义域(-1,+∞)上单调递增.
(2)由(1)知当b>
时函数f(x)无极值点.
当b=
时,f′(x)=
,
∴x∈(-1,-
)时,f′(x)>0,
x∈(-
,+∞)时,f′(x)>0,
∴b=
时,函数f(x)在(-1,+∞)上无极值点.
当b<
时,解f′(x)=0得两个不同解x1=
,x2=
,
∴x1∈(-∞,-1),x2∈(-1,+∞),
此时f(x)在(-1,+∞)上有唯一的极小值点x2=
当0<b<
时,x1,x2∈(-1,+∞)f′(x)在(-1,x1),(x2,+∞)都大于0,
f′(x)在(x1,x2)上小于0,
此时f(x)有一个极大值点x1=
和一个极小值点x2=
,
综上可知,b<0,时,f(x)在(-1,+∞)上有唯一的极小值点x2=
,
当0<b<
时,f(x)有一个极大值点x1=
和一个极小值点x2=
,
b≥
时,函数f(x)在(-1,+∞)上无极值点.
(3)当b=-1时,f(x)=x2-ln(x+1).
令h(x)=x3-x2+ln(x+1),
∴h(x)=
在[0,+∞)上恒正
∴h(x)在[0,+∞)上单调递增,所以当x∈(0,+∞)时,恒有h(x)>h(0)=0,
即当x∈(0,+∞)时,有x3-x2+ln(x+1)>0,ln(x+1)>x2-x3,对任意正整数n,
取x=
得ln(
+1)>
-
.
由f′(x)=
| 2x2+2x+b |
| x+1 |
令g(x)=2x2+2x+b,
则g(x)在(-
| 1 |
| 2 |
| 1 |
| 2 |
∴g(x)min=g(-
| 1 |
| 2 |
| 1 |
| 2 |
当b>
| 1 |
| 2 |
| 1 |
| 2 |
g(x)=2x2+2x+b>0在(-1,+∞)上恒成立,
所以f'(x)>0即当b>
| 1 |
| 2 |
(2)由(1)知当b>
| 1 |
| 2 |
当b=
| 1 |
| 2 |
2(x+
| ||
| x+1 |
∴x∈(-1,-
| 1 |
| 2 |
x∈(-
| 1 |
| 2 |
∴b=
| 1 |
| 2 |
当b<
| 1 |
| 2 |
-1-
| ||
| 2 |
-1+
| ||
| 2 |
∴x1∈(-∞,-1),x2∈(-1,+∞),
此时f(x)在(-1,+∞)上有唯一的极小值点x2=
-1+
| ||
| 2 |
当0<b<
| 1 |
| 2 |
f′(x)在(x1,x2)上小于0,
此时f(x)有一个极大值点x1=
-1-
| ||
| 2 |
-1+
| ||
| 2 |
综上可知,b<0,时,f(x)在(-1,+∞)上有唯一的极小值点x2=
-1+
| ||
| 2 |
当0<b<
| 1 |
| 2 |
-1-
| ||
| 2 |
-1+
| ||
| 2 |
b≥
| 1 |
| 2 |
(3)当b=-1时,f(x)=x2-ln(x+1).
令h(x)=x3-x2+ln(x+1),
∴h(x)=
| 3x3+(x-1)2 |
| x+1 |
∴h(x)在[0,+∞)上单调递增,所以当x∈(0,+∞)时,恒有h(x)>h(0)=0,
即当x∈(0,+∞)时,有x3-x2+ln(x+1)>0,ln(x+1)>x2-x3,对任意正整数n,
取x=
| 1 |
| n |
| 1 |
| n |
| 1 |
| n2 |
| 1 |
| n3 |
点评:本题考察了函数的单调性,函数的极值问题,参数的取值,导数的应用,是一道综合题.

练习册系列答案
相关题目
已知复数z满足|z-i-1|+|z+i-1|=2,则z在复平面内对应的点的轨迹是( )
| A、线段 | B、圆 | C、椭圆 | D、抛物线 |
数列{an}中,an=(-1)nn,则a1+a2+…+a10=( )
| A、10 | B、-10 | C、5 | D、-5 |
用数学归纳法证明:1+
+
+…+
=
时,由n=k到n=k+1左边需要添加的项是( )
| 1 |
| 1+2 |
| 1 |
| 1+2+3 |
| 1 |
| 1+2+3+…+n |
| 2n |
| n+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
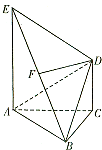 如图,AE⊥平面ABC,CD∥AE,F是BE的中点,已知AC=BC=CD=1,AE=2,∠ACB=90°.
如图,AE⊥平面ABC,CD∥AE,F是BE的中点,已知AC=BC=CD=1,AE=2,∠ACB=90°.