题目内容
已知函数f(x)=(1-2a)x3+(9a-4)x2+(5-12a)x+4a(a∈R).
(1)当a=0时,求函数在区间[0,2]上的最大值;
(2)若函数f(x)在区间[0,2]上的最大值为2,求a的取值范围.
(1)当a=0时,求函数在区间[0,2]上的最大值;
(2)若函数f(x)在区间[0,2]上的最大值为2,求a的取值范围.
考点:二次函数在闭区间上的最值,二次函数的性质
专题:综合题,函数的性质及应用
分析:(1)先求导数f′(x),在函数的定义域内解不等式f′(x)>0,f′(x)<0可求得单调区间,由单调性可求最大值;
(2)讨论满足f′(x)=0的点附近的导数的符号的变化情况,来确定极值,根据极值与最值的求解方法,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,建立等量关系,求出参数a的范围即可.
(2)讨论满足f′(x)=0的点附近的导数的符号的变化情况,来确定极值,根据极值与最值的求解方法,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,建立等量关系,求出参数a的范围即可.
解答:
解:(1)当a=0时,f(x)=x3-4x2+5x,f′(x)=3x2-8x+5=(3x-5)(x-1),
由f′(x)>0,得0≤x<1或
<x≤2;由f′(x)<0,得1<x<
,
∴f(x)在[0,1],[
,2]上单调递增;在[1,
]上单调递减.
又f(1)=f(2)=2,
∴函数在[0,2]上的最大值为2.
(2)一方面由题意,得
,即0≤a≤
;
另一方面,当0≤a≤
时,f(x)=(-2x3+9x2-12x+4)a+x3-4x2+5x,
令g(a)=(-2x3+9x2-12x+4)a+x3-4x2+5x,则
g(a)≤max{g(0),g(
)}
=max{x3-4x2+5x,
(-2x3+9x2-12x+4)+x3-4x2+5x}
=max{x3-4x2+5x,
x2-x+2},
f(x)=g(a)≤max{x3-4x2+5x,
x2-x+2},
又0≤x≤2时,max{x3-4x2+5x}=2,max{
x2-x+2}=2,且f(2)=2,
所以当0≤a≤
时,f(x)在区间[0,2]上的最大值是2.
综上,所求a的取值范围是0≤a≤
.
由f′(x)>0,得0≤x<1或
| 5 |
| 3 |
| 5 |
| 3 |
∴f(x)在[0,1],[
| 5 |
| 3 |
| 5 |
| 3 |
又f(1)=f(2)=2,
∴函数在[0,2]上的最大值为2.
(2)一方面由题意,得
|
| 1 |
| 2 |
另一方面,当0≤a≤
| 1 |
| 2 |
令g(a)=(-2x3+9x2-12x+4)a+x3-4x2+5x,则
g(a)≤max{g(0),g(
| 1 |
| 2 |
=max{x3-4x2+5x,
| 1 |
| 2 |
=max{x3-4x2+5x,
| 1 |
| 2 |
f(x)=g(a)≤max{x3-4x2+5x,
| 1 |
| 2 |
又0≤x≤2时,max{x3-4x2+5x}=2,max{
| 1 |
| 2 |
所以当0≤a≤
| 1 |
| 2 |
综上,所求a的取值范围是0≤a≤
| 1 |
| 2 |
点评:本题主要考查了利用导数研究函数的最值,以及利用导数求闭区间上函数的最值,属于中档题.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的一条渐近线被圆C:x2+y2-6x=0所截得的弦长等于2
,则该双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
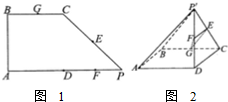 如图1所示,在直角梯形ABCP中,AP∥BC,AP⊥AB,AP=2AB=2BC,D是底边AP的中点,E.F、G分别为PC、PD、CB的中点,将△PCD沿CD折起,使点P位于点P′,且P′D⊥平面ABCD,得折叠后如图2的几何图形.
如图1所示,在直角梯形ABCP中,AP∥BC,AP⊥AB,AP=2AB=2BC,D是底边AP的中点,E.F、G分别为PC、PD、CB的中点,将△PCD沿CD折起,使点P位于点P′,且P′D⊥平面ABCD,得折叠后如图2的几何图形.