题目内容
(理做)已知集合A={x∈R|
≥0},集合B={x∈R|x2-x+m-m2≤0},若A∪B=A,求实数m的取值范围.
| 2-x |
| x+1 |
考点:一元二次不等式的解法,并集及其运算
专题:不等式的解法及应用,集合
分析:化简A、B,由A∪B=A,得B⊆A;由此列出不等式组,求出m的取值范围.
解答:
解:由题意得,A={x∈R|
≤0}=(-1,2],
B={x∈R|x2-x+m-m2≤0}
={x∈R|(x-1+m)(x-m)≤0};
由A∪B=A,得B⊆A;
∴
,
解得-1<m<2,
∴实数m的取值范围是(-1,2).
| x-2 |
| x+1 |
B={x∈R|x2-x+m-m2≤0}
={x∈R|(x-1+m)(x-m)≤0};
由A∪B=A,得B⊆A;
∴
|
解得-1<m<2,
∴实数m的取值范围是(-1,2).
点评:本题考查了集合的运算问题,也考查了不等式的解法与应用问题,是基础题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
设袋中有8个红球,2个白球,若从袋中任取4个球,则其中恰有3个红球的概率为( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
下列四组函数中f(x)与g(x)是同一函数的是( )
A、f(x)=x,g(x)=
| |||||
B、f(x)=(
| |||||
| C、f(x)=2lgx,g(x)=lgx2 | |||||
D、f(x)=|x|,g(x)=
|
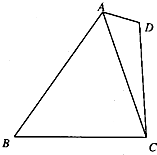 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=