题目内容

用数字2，3组成五位数，且数字2，3至少都出现一次，这样的五位数共有
 
个．（用数字作答）
考点：计数原理的应用
专题：排列组合
分析：首先确定数字中2和3 的个数，当数字中有1个2，4个3时，当数字中有2个2，3个3时，当数字中有3个2，2个3时，当当数字中有4个2，1个3时写出每种情况的结果数，即可求解
解答： 解：首先确定数字中2和3 的个数，
当数字中有1个2，4个3时，共有C51=5种结果，
当数字中有2个2，3个3时，共有C52=10种结果，
当数字中有3个2，2个3时，共有有C51=10种结果，
当数字中有4个2，1个3时，共有C51=5种结果，
根据分类加法原理知共有5+10+10+5=30种结果，
故答案为：30．
点评：本题考查分类计数原理，注意分类时要做到不重不漏，本题是一个基础题
练习册系列答案
相关题目
设函数f（x）=lnx+
m
x
，m∈R
（1）当m=e（e为自然对数的底数）时，求f（x）的最小值；
（2）讨论函数g（x）=f′（x）-
x
3
零点的个数；
（3）（理科）若对任意b＞a＞0，
f(b)-f(a)
b-a
＜1恒成立，求m的取值范围．
设曲线C：f（x）=lnx-ex（e=2.71829…），f′（x）表示f（x）的导函数．
（Ⅰ）求函数f（x）的极值；
（Ⅱ）数列{an}满足a1=e，an+1=2f′（
1
an
）+3e，求证：数列{an}中的任意三项都不能构成等差数列；
（Ⅲ）对于曲线C上的不同两A（x1，y1），B（x2，y2）（0＜x1＜x2），是否存在唯一x0∈（x1，x2），使直线AB的斜率等于f′（x0）？证明的结论．
已知
3sinα+cosα
3cosα-sinα
=2，则2+3sin（α-3π）sin（
3π
2
-α）-cos2（-α）的值为
 
．
已知向量|
a
|=2，|
b
|=
3
，且
a
•
b
=3，则
a
与
b
的夹角为
 
．
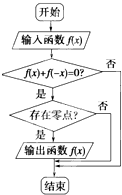某程序框图如图所示，现输入四个函数（1）f（x）=x2，（2）f（x）=
1
x
，（3）f（x）=ln x+2x-6，（4）f（x）=sin x，则输出函数是
 
．
已知函数f（x）是定义在[-2，2]上的奇函数，且当0≤x≤2时，f（x）=x2+x，若f（m+1）≥f（1-m），则实数m的取值范围是
 
．
设p：“-1＜x＜3”，q：“x2-3x＜0”，p是q的
 
条件（用“充分不必要，必要不充分，充要，既不充分也不必要”填空）
若函数f（x）=loga（2-ax）（a＞0，a≠1）在区间（1，3）内单调递增，则a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网