题目内容
8.已知x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$,若2x+y+k≥0恒成立,则直线2x+y+k=0被圆(x-1)2+(y-2)2=25截得的弦长的最大值为( )| A. | 10 | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{5}$ | D. | 3$\sqrt{5}$ |
分析 由约束条件作出可行域,求出2x+y的最小值,结合2x+y+k≥0恒成立求得k的范围,再由直线与圆的关系可得当k=6时,直线2x+y+k=0被圆(x-1)2+(y-2)2=25截得的弦长最大,从而求得最大值.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$作出可行域如图,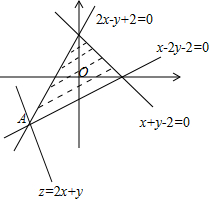
联立$\left\{\begin{array}{l}{2x-y+2=0}\\{x-2y-2=0}\end{array}\right.$,解得A(-2,-2),
令z=2x+y,化为y=-2x+z,由图可知,当直线y=-2x+z过A时,直线在y轴上的截距最小,z有最小值为-6.
由2x+y+k≥0恒成立,得-k≤2x+y恒成立,即-k≤-6,则k≥6.
圆(x-1)2+(y-2)2=25的圆心(1,2)到直线2x+y+k=0的距离d=$\frac{|4+k|}{\sqrt{5}}$,当k≥6时,d$≥2\sqrt{5}$.
∴当d=$2\sqrt{5}$时,直线2x+y+k=0被圆(x-1)2+(y-2)2=25截得的弦长最大,为2$\sqrt{{5}^{2}-(2\sqrt{5})^{2}}=2\sqrt{5}$.
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
19.执行如图所示的程序框图,输出的x的值为( )


| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
3.下列说法错误的是( )
| A. | 回归直线过样本点的中心($\overline{x}$,$\overline{y}$) | |
| B. | 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1 | |
| C. | 对分类变量X与Y,随机变量K2的观测值越大,则判断“X与Y有关系”的把握程度越小 | |
| D. | 在回归直线方程$\stackrel{∧}{y}$=0.2x+0.8中,当解释变量x每增加1个单位时预报变量$\stackrel{∧}{y}$平均增加0.2个单位 |
13.设sin(π-θ)=$\frac{1}{3}$,则cos2θ=( )
| A. | ±$\frac{4\sqrt{2}}{9}$ | B. | $\frac{7}{9}$ | C. | -$\frac{4\sqrt{2}}{9}$ | D. | -$\frac{7}{9}$ |
18.设抛物线的顶点在原点,其焦点在x轴上,又抛物线上的点A(-1,a)与焦点F的距离为2,则a=( )
| A. | 4 | B. | 4或-4 | C. | -2 | D. | -2或2 |