题目内容
18.已知椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1的右焦点F到双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线的距离小于$\sqrt{3}$,则双曲线E的离心率的取值范围是1<e<2.分析 求出椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1的右焦点F的坐标,双曲线的渐近线方程,由点到直线的距离公式,可得a,b的关系,再由离心率公式,计算即可得到.
解答 解:椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1的右焦点F为(2,0),
双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线为bx+ay=0,
则焦点到渐近线的距离d=$\frac{2b}{\sqrt{{b}^{2}+{a}^{2}}}$<$\sqrt{3}$,
即有2b<$\sqrt{3}$c,
∴4b2<3c2,
∴4(c2-a2)<3c2,
∴e<2,
∵e>1,
∴1<e<2.
故答案为1<e<2.
点评 本题考查抛物线和双曲线的方程和性质,考查渐近线方程的运用,考查点到直线的距离公式,考查离心率的求法,属于中档题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
8.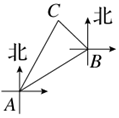 如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
 如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.| A. | 5($\sqrt{6}$+$\sqrt{2}$) | B. | 5($\sqrt{6}$-$\sqrt{2}$) | C. | 10($\sqrt{6}$+$\sqrt{2}$) | D. | 10($\sqrt{6}$-$\sqrt{2}$) |
6.已知函数y=2sin(x+$\frac{π}{2}$)cos(x-$\frac{π}{2}$)与直线y=$\frac{1}{2}$相交,若在y轴右侧的交点自左向右依次记为M1,M2,M3,…,则|$\overrightarrow{{M}_{1}{M}_{12}}$|等于( )
| A. | $\frac{16π}{3}$ | B. | 6π | C. | $\frac{17π}{3}$ | D. | 12π |
13.若a=($\frac{1}{2}$)${\;}^{\frac{1}{5}}$,b=($\frac{1}{5}$)${\;}^{-\frac{1}{2}}$,c=log${\;}_{\frac{1}{5}}$10,则a,b,c大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
10.已知抛物线C1:y2=8ax(a>0),直线l倾斜角是45°且过抛物线C1的焦点,直线l被抛物线C1截得的线段长是16,双曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一个焦点在抛物线C1的准线上,则直线l与y轴的交点P到双曲线C2的一条渐近线的距离是( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
8.已知x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$,若2x+y+k≥0恒成立,则直线2x+y+k=0被圆(x-1)2+(y-2)2=25截得的弦长的最大值为( )
| A. | 10 | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{5}$ | D. | 3$\sqrt{5}$ |