题目内容
13.设sin(π-θ)=$\frac{1}{3}$,则cos2θ=( )| A. | ±$\frac{4\sqrt{2}}{9}$ | B. | $\frac{7}{9}$ | C. | -$\frac{4\sqrt{2}}{9}$ | D. | -$\frac{7}{9}$ |
分析 利用诱导公式求得sinθ的值,再利用二倍角公式求得cos2θ的值.
解答 解:∵sin(π-θ)=sinθ=$\frac{1}{3}$,则cos2θ=1-2sin2θ=1-2•$\frac{1}{9}$=$\frac{7}{9}$,
故选:B.
点评 本题主要考查利用诱导公式、二倍角公式进行化简求值,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
4.在区间[0,8]上随机取一个x的值,执行如图的程序框图,则输出的y≥3的概率为( )


| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
8.已知x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$,若2x+y+k≥0恒成立,则直线2x+y+k=0被圆(x-1)2+(y-2)2=25截得的弦长的最大值为( )
| A. | 10 | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{5}$ | D. | 3$\sqrt{5}$ |
18.已知函数f(x)=$\frac{{e}^{x}}{x}-kx$(e为自然对数的底数)有且只有一个零点,则实数k的取值范围是( )
| A. | (0,2) | B. | (0,$\frac{{e}^{2}}{4}$) | C. | (0,e) | D. | (0,+∞) |
5.已知A为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上一点,B为点A关于原点的对称点,F为椭圆的左焦点,且AF⊥BF,若∠ABF∈[$\frac{π}{12}$,$\frac{π}{4}$],则该椭圆离心率的取值范围为( )
| A. | [0,$\frac{\sqrt{2}}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,1) | C. | [0,$\frac{\sqrt{6}}{3}$] | D. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{6}}{3}$] |
2.已知集合M={-1,0,1,2,3},N={x|x2-2x>0},则M∩N=( )
| A. | {3} | B. | {2,3} | C. | {-1,3} | D. | {0,1,2} |
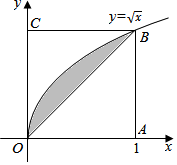 如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.
如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.