题目内容
7．求下列函数的导数：（1）y=$\frac{3{x}^{2}-x\sqrt{x}+5\sqrt{x}-9}{\sqrt{x}}$；
（2）f（x）=（x-1）（x+1）（x2+1）（x4+1）
分析 先化简，再根据导数的运算法则求导即可．
解答 解：（1）y=$\frac{3{x}^{2}-x\sqrt{x}+5\sqrt{x}-9}{\sqrt{x}}$=3${x}^{\frac{3}{2}}$-x+5-9${x}^{-\frac{1}{2}}$，
∴y′=$\frac{9}{2}$x${\;}^{\frac{1}{2}}$-1+$\frac{9}{2}{x}^{-\frac{3}{2}}$，
（2）f（x）=（x-1）（x+1）（x2+1）（x4+1）=（x2-1）（x2+1）（x4+1）=（x4-1）（x4+1）=x8-1，
∴f′（x）=8x7．
点评 本题考查了导数的运算法则，关键是掌握导数基本公式．
练习册系列答案
相关题目
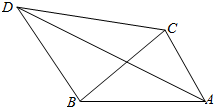如图，在△ABC中，AB=$\sqrt{2}$，AC=1，以BC为边作等腰直角三角形BCD（B为直角顶点，A，D两点在直线BC的两侧），当∠A∈[$\frac{π}{6}$，$\frac{2π}{3}$]时，$\overrightarrow{AC}$•$\overrightarrow{AD}$的取值范围是[$\frac{\sqrt{6}-\sqrt{2}}{2}$，2]．
2．已知A（1，1，2），B（-1，2，1），O为坐标原点，则向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角是（ ）
| A． | 0 | B． | $\frac{π}{3}$ | C． | π | D． | $\frac{π}{2}$ |
12．函数f（x）=2x-2+ex-1的零点所在区间为（ ）
| A． | （-1，0） | B． | （0，1） | C． | （1，2） | D． | （2，3） |