题目内容
15.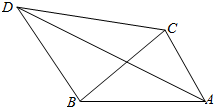 如图,在△ABC中,AB=$\sqrt{2}$,AC=1,以BC为边作等腰直角三角形BCD(B为直角顶点,A,D两点在直线BC的两侧),当∠A∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,$\overrightarrow{AC}$•$\overrightarrow{AD}$的取值范围是[$\frac{\sqrt{6}-\sqrt{2}}{2}$,2].
如图,在△ABC中,AB=$\sqrt{2}$,AC=1,以BC为边作等腰直角三角形BCD(B为直角顶点,A,D两点在直线BC的两侧),当∠A∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,$\overrightarrow{AC}$•$\overrightarrow{AD}$的取值范围是[$\frac{\sqrt{6}-\sqrt{2}}{2}$,2].
分析 运用正弦定理,可得BDsin∠ABC=sin∠BAC,再由余弦定理可得AD2=5+2$\sqrt{2}$•sin∠BAC-2$\sqrt{2}$cos∠BAC,由向量的数量积的定义可得$\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|•|$\overrightarrow{AD}$|•cos∠CAD=$\frac{1}{2}$(AC2+AD2-CD2)=2sin($\frac{π}{4}$+∠BAC),由A的范围,结合正弦函数的性质可得取值范围.
解答 解:△ABC中,AB=$\sqrt{2}$,AC=1,
∵BC=BD,
∴在△ABC中,由正弦定理得
$\frac{AC}{sin∠ABC}$=$\frac{AB}{sin∠ACB}$=$\frac{BD}{sin∠BAC}$,
∴BDsin∠ABC=sin∠BAC,
在△BAD中,AD2=BD2+AB2-2BD•BAcos(90°+∠ABC)
=BC2+2+2BC•$\sqrt{2}$sin∠ABC
=(AC2+AB2-2AC•AB•cos∠BAC)+2+2$\sqrt{2}$•BCsin∠ABC
=(1+2-2$\sqrt{2}$cos∠BAC)+2+2$\sqrt{2}$•BDsin∠ABC
=(1+2-2$\sqrt{2}$cos∠BAC)+2+2$\sqrt{2}$•sin∠BAC
=5+2$\sqrt{2}$•sin∠BAC-2$\sqrt{2}$cos∠BAC
$\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|•|$\overrightarrow{AD}$|•cos∠CAD=$\frac{1}{2}$(AC2+AD2-CD2)
=$\frac{1}{2}$(1+5+2$\sqrt{2}$•sin∠BAC-2$\sqrt{2}$cos∠BAC-6+4$\sqrt{2}$cos∠BAC)
=$\sqrt{2}$(sin∠BAC+cos∠BAC)=2sin($\frac{π}{4}$+∠BAC),
由∠A∈[$\frac{π}{6}$,$\frac{2π}{3}$],即有$\frac{π}{4}$+∠BAC∈[$\frac{5π}{12}$,$\frac{11π}{12}$],
则sin($\frac{π}{4}$+∠BAC)∈[$\frac{\sqrt{6}-\sqrt{2}}{4}$,1],
则$\overrightarrow{AC}$•$\overrightarrow{AD}$的取值范围是[$\frac{\sqrt{6}-\sqrt{2}}{2}$,2].
故答案为:[$\frac{\sqrt{6}-\sqrt{2}}{2}$,2].
点评 本题考查向量的数量积的定义,考查解三角形中的正弦定理和余弦定理的运用,同时考查诱导公式和两角和的正弦公式的运用,属于中档题.

 智能训练练测考系列答案
智能训练练测考系列答案| A. | 18 | B. | 12 | C. | 9 | D. | 6 |
| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\sqrt{2}$ |
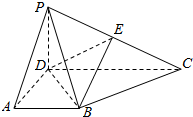 四棱锥P-ABCD中,直角梯形ABCD中,AD⊥CD,AB∥CD,∠APD=60°,PA=CD=2PD=2AB=2,且平面PDA⊥平面ABCD,E为PC的中点.
四棱锥P-ABCD中,直角梯形ABCD中,AD⊥CD,AB∥CD,∠APD=60°,PA=CD=2PD=2AB=2,且平面PDA⊥平面ABCD,E为PC的中点.