题目内容
17.阶梯教室安装的连体课桌一行坐5个人,考生只能从课桌两头走出考场,考生交卷的时间先后不一,如果坐在里面的考生先要交卷就需要打扰别人,把一行考生中打扰别人交卷的人数视为随机变量X,试求X的分布列和数学期望.分析 由题意X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:由题意知X的所有可能取值为0,1,2,3,
P(X=0)=$\frac{{2}^{4}}{{A}_{5}^{5}}$=$\frac{16}{120}$,
P(X=1)=$\frac{{C}_{3}^{1}•{2}^{3}+{C}_{2}^{1}•{2}^{2}+{2}^{4}}{{A}_{5}^{5}}$=$\frac{48}{120}$,
P(X=2)=$\frac{{C}_{2}^{1}•{2}^{3}+{C}_{3}^{1}•{2}^{2}+{2}^{4}}{{A}_{5}^{5}}$=$\frac{44}{120}$,
P(X=3)=$\frac{{A}_{3}^{3}×2}{{A}_{5}^{5}}$=$\frac{12}{120}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{16}{120}$ | $\frac{48}{120}$ | $\frac{44}{120}$ | $\frac{12}{120}$ |
点评 本题考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
7.在等差数列{an}中,a2+a5=19,S5=40,则a1=( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
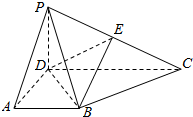 四棱锥P-ABCD中,直角梯形ABCD中,AD⊥CD,AB∥CD,∠APD=60°,PA=CD=2PD=2AB=2,且平面PDA⊥平面ABCD,E为PC的中点.
四棱锥P-ABCD中,直角梯形ABCD中,AD⊥CD,AB∥CD,∠APD=60°,PA=CD=2PD=2AB=2,且平面PDA⊥平面ABCD,E为PC的中点.