题目内容

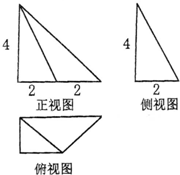
某几何体的三视图如图所示，则该几何体的体积为
 
．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得，该几何是一个以俯视图为底面的棱锥，分别求出底面面积和高，代入棱锥体积公式，可得答案．
解答： 解：由已知中的三视图可得，该几何是一个以俯视图为底面的棱锥，
∵底面是一个上下底边长为2和4，高为2的梯形，
故底面面积S底=
1
2
×(2+4)×2=6，
棱锥的高h=4，
故棱锥的体积V=
1
3
S底h=
1
3
×6×4=8，
故答案为：8．
点评：本题考查的知识点是由三视图求体积，其中分析出几何体的形状是解答的关键．
练习册系列答案
相关题目
2014年4月10日至12日，第七届中国西部国际化工博览会在成都举行，为了使志愿者更好的服务于大会，主办方决定对40名志愿者进行一次考核，考核分为两个科目：“成都文化”和“志愿者知识”，其中“成都文化”的考核成绩分为10分，8分，6分，4分共四个档次，“志愿者知识”的考核结果分为A，B，C，D共四个等级．这40名志愿者的考核结果如下表：
10分 8分 6分 4分
A 1 5 7 0
B 2 1 7 1
C 2 0 6 3
D 2 1 2 0
（Ⅰ）求“成都文化”考核成绩的平均值（结果用小数表示）
（Ⅱ）从“成都文化”考核成绩为10分的志愿者中任意选2名作为队长，求队长中至少有一个人的“志愿者知识”考核等级为A或B的概率．
已知
AB
=
a
+5
b
，
BC
=-2
a
+8
b
，
CD
=3
a
-3
b
，则A、B、C、D四点中一定共线的三点是
 
．
在△ABC中，B=60°，AC=
3
，AB+BC的最大值为
 
．
已知样本2000个，其频率分布直方图如下，那么在[2，8）之间的有
 
个．
若关于x的不等式-
1
2
x2+2x＞-mx-
1
2
的解集为{x|0＜x＜2}，则m=
 
．
△ABC的内角为A，B，C，若sinA=cosB=
3
5
，则
∫
C
0
|sinx-cosx|dx的值为
 
．
已知集合A={x|x2-1＜0}，B={x|x＜m}，若“a∈A”是“a∈B”的充分而不必要条件，则实数m的取值可以是（　　）
A、
1
4
B、
1
3
C、1
D、
1
2
已知函数f（x）=x2+2a1og2（x2+2）+a2-3有且只有一个零点，则实数a的值为（　　）
A、1B、-3C、2D、1或-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网