题目内容
11.已知矩阵A=$[\begin{array}{l}{a}&{3}\\{2}&{d}\end{array}]$,若A$[\begin{array}{l}{1}\\{2}\end{array}]$=$[\begin{array}{l}{8}\\{4}\end{array}]$,求矩阵A的特征值.分析 利用矩阵的乘法,求出a,d,利用矩阵A的特征多项式为0,求出矩阵A的特征值.
解答 解:因为A$[\begin{array}{l}{1}\\{2}\end{array}]$=$[\begin{array}{l}{a+6}\\{2+2d}\end{array}]$=$[\begin{array}{l}{8}\\{4}\end{array}]$,
所以$\left\{\begin{array}{l}{a+6=8}\\{2+2d=4}\end{array}\right.$,解得a=2,d=1.
所以矩阵A的特征多项式为f(λ)=$|\begin{array}{l}{λ-2}&{-3}\\{-2}&{λ-1}\end{array}|$=(λ-2)(λ-1)-6=(λ-4)(λ+1),
令f(λ)=0,解得矩阵A的特征值为λ=4或-1.
点评 本题考查矩阵的乘法,考查矩阵A的特征值,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{-x}+a,x≤0}\\{(x-1)^{3}+1,x>0}\end{array}$,且?x0∈[2,+∞)使得f(-x0)=f(x0),则实数a的取值范围为( )
| A. | (-∞,2-$\sqrt{2}$] | B. | [2-$\sqrt{2}$,+∞) | C. | (-∞,2-$\sqrt{2}$) | D. | (2-$\sqrt{2}$,+∞) |
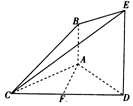 如图,在梯形ADEB中,AB∥DE,AD=DE=2AB,△ACD是正三角形,AB⊥平面ACD,且F是CD的中点.
如图,在梯形ADEB中,AB∥DE,AD=DE=2AB,△ACD是正三角形,AB⊥平面ACD,且F是CD的中点.