题目内容
2．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{-x}+a，x≤0}\\{（x-1）^{3}+1，x＞0}\end{array}$，且?x0∈[2，+∞）使得f（-x0）=f（x0），则实数a的取值范围为（ ）| A． | （-∞，2-$\sqrt{2}$] | B． | [2-$\sqrt{2}$，+∞） | C． | （-∞，2-$\sqrt{2}$） | D． | （2-$\sqrt{2}$，+∞） |
分析 f（x）=（x-1）3+1（x＞0）关于y轴对称的函数解析式为f（x）=-（x+1）3+1（x＜0），则由题意，x≤-2时，f（x）=-（x+1）3+1（x＜0），与g（x）=$\sqrt{-x}$+a有交点，可得$\sqrt{2}$+a≥-（-2+1）3+1，即可求出实数a的取值范围．
解答 解：f（x）=（x-1）3+1（x＞0）关于y轴对称的函数解析式为f（x）=-（x+1）3+1（x＜0），
则由题意，x≤-2时，f（x）=-（x+1）3+1（x＜0），与g（x）=$\sqrt{-x}$+a有交点，
∴$\sqrt{2}$+a≥-（-2+1）3+1，∴a≥2-$\sqrt{2}$，
故选B．
点评 本题考查分段函数，考查函数解析式的求解，正确转化是关键．
练习册系列答案
相关题目
如图，棱柱ABCD-A1B1C1D1中，底面ABCD是平行四边形，侧棱AA1⊥底面ABCD，AB=1，AC=$\sqrt{3}$，BC=BB1=2．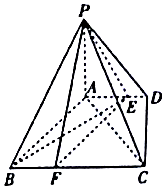
如图，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是直角梯形，∠ADC=90°，AD∥BC，AB⊥AC，AB=AC=$\sqrt{2}$，点E在AD上，且AE=2ED．