题目内容

1．已知函数f（x）=$\left\{\begin{array}{l}{|lo{g}_{4}x|，0＜x≤4}\\{-x+5，x＞4}\end{array}\right.$若关于x的方程f（x）-m=0有三个不相等的实数解x1，x2，x3，则x1•x2•x3的取值范围是（4，5）．

分析 作出f（x）的函数图象，得出三个解得范围，根据对数的运算性质得出x1x2=1，故x3的范围即为所求．

解答 解：f（x）=$\left\{\begin{array}{l}{-lo{g}_{4}x，0＜x＜1}\\{lo{g}_{4}x，1＜x≤4}\\{-x+5，x＞4}\end{array}\right.$，
作出f（x）的函数图象如图所示：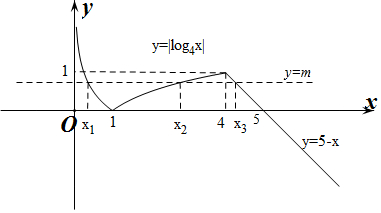

不妨设x1＜x2＜x3，则0＜x1＜1，1＜x2＜4，x3＞4
由图象可知4＜x3＜5，且-log4x1=log4x2，
∴log4x2+log4x1=log4（x1x2）=0，即x1x2=1，
∴x1x2x3=x3．
∴x1•x2•x3的取值范围是（4，5）．
故答案为：（4，5）．

点评 本题考查了方程的解与函数图象的关系，对数的运算性质，属于中档题．

练习册系列答案
相关题目
11．已知矩阵A=$[\begin{array}{l}{a}&{3}\\{2}&{d}\end{array}]$，若A$[\begin{array}{l}{1}\\{2}\end{array}]$=$[\begin{array}{l}{8}\\{4}\end{array}]$，求矩阵A的特征值．
12．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左，右焦点分别为F1，F2，过F1任作一条与两坐标轴都不垂直的直线，与C交于A，B两点，且△ABF2的周长为8．当直线AB的斜率为$\frac{3}{4}$时，AF2与x轴垂直．
（I）求椭圆C的方程；
（Ⅱ）在x轴上是否存在定点M，总能使MF1平分∠AMB？说明理由．
9．已知数列{an}的前n项和为Sn，且a1=1，an+1=$\left\{\begin{array}{l}{{a}_{n}+3，\frac{n}{3}∉N*}\\{{a}_{n}，\frac{n}{3}∈N*}\end{array}\right.$，则S3n=9n2+3n．
16．i是虚数单位，复数z=$\frac{3i}{1+i}$的虚部是$\frac{3}{2}$．
6．已知函数f（x）=x3-3a2x+2a2+1（a≥0）
（Ⅰ）求f（x）的单调区间；
（Ⅱ）讨论函数f（x）在区间（-2，3）内极值点的个数；
（Ⅲ）证明：当0≤x≤1时，f（x）+|1-a2|≥1．
13．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F（c，0），过点F且斜率为-$\frac{b}{a}$的直线与双曲线的渐近线交于点A，若△OAF的面积为4ab（O为坐标原点），则双曲线的离心率为（　　）
A．$\sqrt{2}$B．$\sqrt{3}$C．2D．4
10．已知定义在R上的函数f（x）=2|x-m|-1（m为实数）为偶函数，记a=f（log0.53），b=f（log25），c=f（2m），则a，b，c的大小关系为（　　）
A．a＜b＜cB．c＜b＜aC．a＜c＜bD．c＜a＜b
19．已知平面内两点A（0，-a），B（0，a）（a＞0），有一动点P在平面内，且直线PA与直线PB的斜率分别为k1，k2，令k1•k2=m，其中m≠0．
（Ⅰ）求点P的轨迹方程；
（Ⅱ）已知N点在圆x2+y2=a2上，设m∈（-1，0）时对应的曲线为C，设F1，F2是该曲线的两个焦点，试问是否存在点N，使△F1NF2的面积S=$\sqrt{-m}$•a2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网